You get a bonus - 1 coin for daily activity. Now you have 1 coin

Numeric and alphabetic expressions

Lecture



For the correct solution of equations, you need to be able to use mathematical language. The words of a mathematical language are numeric and alphabetic expressions .

Mathematical expressions can consist of one number or one letter:

  • 42
  • z

Or from two or more numbers and letters connected by signs of arithmetic operations:

  • a - 4
  • 2x
  • x + y

Equality and inequality signs are never used in writing expressions.

(=; ≠;>; <; ≥; ≤)

The signs above are used to record equalities and inequalities.

Mathematical expressions are divided into numeric and alphabetic.

An expression is called numeric if it does not contain letters. Examples of numeric expressions:

  • eight
  • 3 • 4
  • 5: 1
  • 41 + 2 • 3

If you perform all the actions contained in a numerical expression, you get the numerical value of the expression .

Example:

The record 30 • 5 + 40 is a numeric expression.

Having executed all actions, we will receive number 190 - numerical value of expression.

If any number in a numerical expression is replaced by a letter, then the resulting expression is called alphabetic .

  • 7t + 5
  • ab - c
  • 25: 5 - y

The numerical factor (coefficient) is always written before the letter.

The multiplication sign between a number and a letter is usually not written.

  • 3x + 5y
  • 5abc

The multiplication sign is not written in cases where one of the factors is placed before or after the bracket, or both factors are expressed in letters.

  • 3 (t + n)
  • xn

How are literal expressions read

The letter expressions are read as follows.

  • 4a - four a
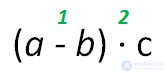  • More complex expressions begin to read on the last performed action. Consider the letter expression below. Numeric and alphabetic expressions The last action in this expression is multiplication. Therefore, we read the expression as follows: the product of the difference of the numbers a and b [b] by the number c [c].

In alphabetic expression, lowercase Latin letters may denote different numbers.

The number with which we replace the lowercase Latin letter when calculating, is the meaning of the letter in the literal expression. Depending on the example setting, such values ​​for the same letter may be several.

The task of the textbook "Vilenkin 5 class"


No. 336 (a)

Find the value of the expression :

a) a + 7 483, if a = 567; 2 415;

Instead of the letter “a” we substitute the data in the task of its value. First the first value, then the second.

  • 567 + 7,483 = 8,050
  • 2,415 + 7,483 = 9,898

Comments

To leave a comment
If you have any suggestion, idea, thanks or comment, feel free to write. We really value feedback and are glad to hear your opinion.
To reply

Arithmetic

Terms: Arithmetic