Finding the greatest common divisor (GCD)

If a natural number is divisible by only 1 and by itself, then it is called simple.

Any natural number is always divisible by 1 and by itself.

The number 2 is the smallest prime number. This is the only even prime number, the other primes are odd.

There are many prime numbers, and the first among them is the number 2. However, there is no last prime number. In the "For study" section you can download a table of prime numbers up to 997.

But many natural numbers are divided completely into other natural numbers.

For example:

• the number 12 is divisible by 1, by 2, by 3, by 4, by 6, by 12;
• the number 36 is divided by 1, by 2, by 3, by 4, by 6, by 12, by 18, by 36.

The numbers into which the number is completely divided (for 12 it is 1, 2, 3, 4, 6 and 12) are called the divisors of the number.

A natural number that has more than two dividers is called composite.

Note that the numbers 12 and 36 have common divisors. These are the numbers: 1, 2, 3, 4, 6, 12. The greatest divisor of these numbers is 12.

The common divisor of the two given numbers a and b is the number by which both given numbers a and b are divided without remainder.

Briefly, the greatest common divisor of the numbers a and b is written as :

Gcd (a; b).

Example: GCD (12; 36) = 12.

Divisors of numbers in the record of the decision are denoted by a capital “D”.

Example.

Numbers 7 and 9 have only one common divisor - number 1. Such numbers are called mutually prime numbers .

How to find the greatest common factor

To find the GCD of two or more natural numbers you need:

1. decompose the divisors of numbers into prime factors;

Calculations are conveniently recorded with a vertical bar. To the left of the stroke, first write the dividend, to the right, the divisor. Further, in the left column, write the values ​​of the quotients.

Let us explain at once with an example. We decompose the numbers 28 and 64 into prime factors.

2. We underline the same prime factors in both numbers.
   28 = 2 • 2 • 7
   
   64 = 2 • 2 • 2 • 2 • 2 • 2
3. Find the product of the same simple factors and record the answer;
   GCD (28; 64) = 2 • 2 = 4
   
   Answer: NOD (28; 64) = 4

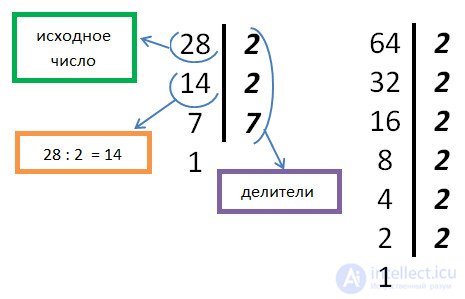
There are two ways to make a finding for NOD: in a column (as was done above) or in a line.

The first way to write gcd

Find GCD 48 and 36.

The second way to write gcd

Now we will write down the solution of the NOD search in a line. Find the gcd 10 and 15.