Lecture
From the permutation of the multipliers the product does not change.
a • b = b • a
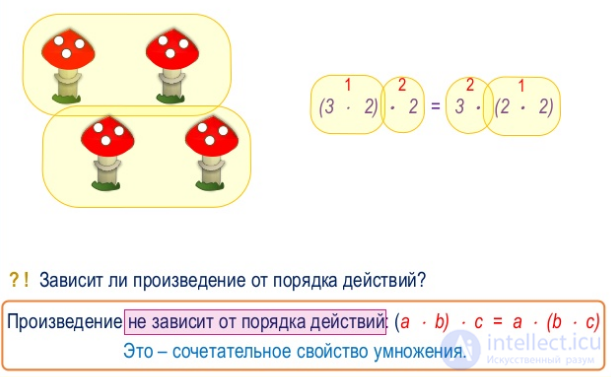
To multiply a number by the product of two numbers, you can first multiply it by the first factor, and then multiply the resulting product by the second factor.
a • (b • c) = (a • b) • c
The transfer and combination properties of multiplication allow us to formulate a rule for the transformation of products.
When multiplying several numbers, you can rearrange them as you like and merge them into groups.
If at least one factor in a product is zero, then the product itself will be zero.
a • 0 = 0
0 • a • b • c = 0
To multiply the sum by a number, you can multiply each term by this number and add the results.
(a + b) • c = a • c + b • c
This property holds for any number of terms.
(a + b + c + d) • k = a • k + b • k + c • k + d • k
To multiply the difference by a number, you can multiply by this number, first decremented and then subtracted, and subtract the second from the first work.
In literal form, the property is written as:
(a - b) • c = a • c - b • c
To multiply a number by the product of two numbers, you can first multiply it by the first factor, and then multiply the resulting product by the second factor.


If the dividend and the divisor are multiplied or divided by the same natural number, then their quotient will not change.
a: b = (a • k): (b • k), where k is any natural number.
Please note that the property of division above allows us to reduce fractions.
Using all the above properties allows us to simplify expressions.
Comments
To leave a comment
Arithmetic
Terms: Arithmetic