Lecture
not all ordinary fractions can be represented as a final decimal fraction.
For example, if we divide 2 by 3, we first get zero integers, then six tenths, and then when we divide, the remainder 2 will be repeated all the time, and in private - the number 6.
Such a division cannot be completed without remainder, and therefore a 2/3 fraction cannot be represented as a final decimal fraction.
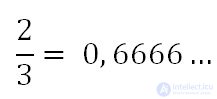
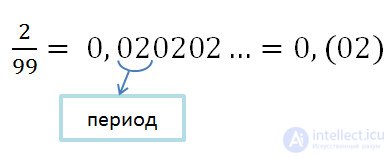
If a single digit or group of numbers in the decimal fraction begins to repeat infinitely many times, such a fraction is called a recurring fraction .
In a brief record of a periodic fraction, a repeating number (or group of numbers) is written in brackets. This number (or group of numbers) is called the fraction period .
Instead of 0.666 ... they write 0, (6) and read "zero zero and six in the period".
Periodic infinite decimal fraction can be converted to ordinary fraction .
Consider a periodic fraction of 10.0219 (37).
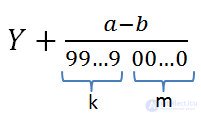
So, we substitute all found values in the formula above and we receive an ordinary fraction. The received answer can always be checked on a regular calculator.
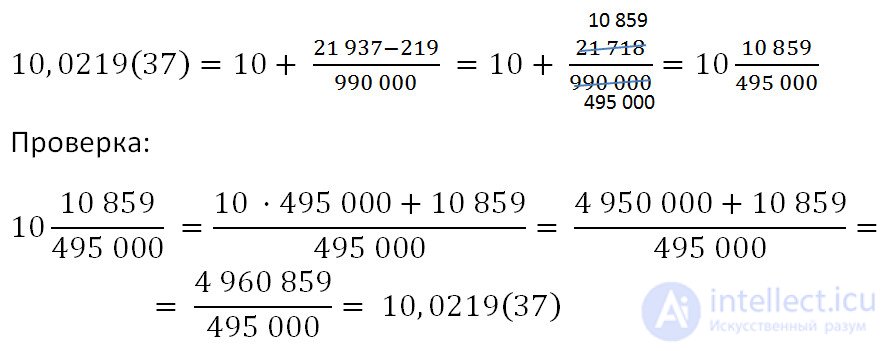
Comments
To leave a comment
Arithmetic
Terms: Arithmetic