Lecture
It is convenient to perform the addition of numbers of small modulus on a coordinate line, mentally imagining how a point denoting a number moves along a number axis.
Take some number, for example, 3. We denote it on the number axis by point A.
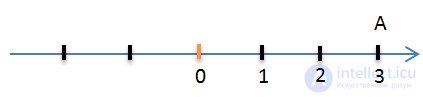
Let us add the positive number 2 to the number. This will mean that the point A should be moved to two unit segments in the positive direction, that is, to the right. As a result, we get point B with coordinate 5.
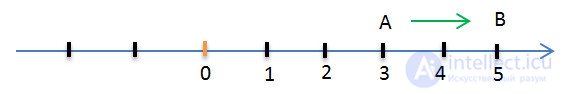 3 + (+ 2) = 5
3 + (+ 2) = 5In order to add a negative number (- 5) to a positive number, for example, to 3, point A should be moved 5 units of length in the negative direction, that is, to the left.
In this case, the coordinate of point B is equal to - 2.

So, the order of addition of rational numbers using the number axis will be as follows:
Example.
- 2 + (- 6) =Moving from the point - 2 to the left (since there is a minus sign in front of 6), we get - 8.
 - 2 + (- 6) = - 8
- 2 + (- 6) = - 8It is easier to add rational numbers if you use the concept of a module.
Let us need to add the numbers that have the same signs.
For this, we discard the signs of numbers and take the modules of these numbers. We add the modules and put a sign before the sum, which was common to the given numbers.
Example.
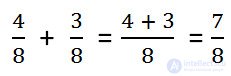
An example of the addition of negative numbers.
(- 3.2) + (- 4.3) = - (3.2 + 4.3) = - 7.5In order to add the numbers of a single character, it is necessary to add their modules and put in front of the sum a character that was before the components.
If the numbers have different signs, then we act somewhat differently than when adding numbers with the same signs.
An example of the addition of negative and positive numbers .
0.3 + (- 0.8) = - (0.8 - 0.3) = - 0.5An example of the addition of mixed numbers.
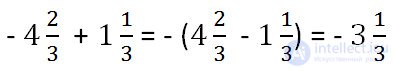
To add the numbers of a different sign :
Comments
To leave a comment
Arithmetic
Terms: Arithmetic