Lecture
The concept of scale is closely related to the ratio of numbers and proportions. Therefore, if you are not confident in your knowledge of these topics, we strongly recommend that you study them again.
You can do this on our resource in the topics of the ratio of numbers and proportions.
Scale is an important concept. If you learn to understand him correctly, he will help you not only in mathematics, but also in geography, drawing, and sometimes in physics.
The scale is the ratio of the length of a segment on the map to the length of the corresponding segment on the ground (in reality).
The scale is recorded as the ratio of two numbers. The first term of the relationship is usually 1, and the second term is a number indicating how many times the length of a distance unit (cm, m or km) on the map is less than the corresponding distance unit in reality.
Let's look at an example:
Below is a part of the map with a scale of 1: 10 000 000 (cm). Such a scale means that 10,000,000 (cm) real distance, or 100,000 (m), or 100 (km) is placed on a map of 1 cm.
It is said that the map is made on the scale of one-millionth (by the name of the decimal fraction, into which the ratio 1: 10 000 000 = 0.000 000 01 can turn.
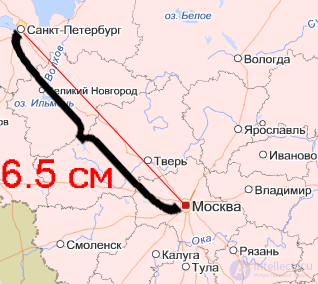
St. Petersburg and Moscow on the map are connected by a length of 6.5 (cm).
Determine how much in reality (km) between Moscow and St. Petersburg.
To solve this problem, we will compile a table and enter the necessary data into it. The unknown value is denoted by x.
| On the map | In the reality | |
|---|---|---|
| Scale | 1 (cm) | 10,000,000 (cm) |
| Distance between Moscow and Petersburg | 6.5 (cm) | x (cm) |
Compose and decide the proportion:
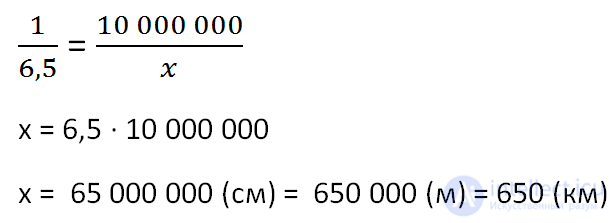
Answer: 650 km is the approximate distance between Moscow and St. Petersburg.
Now, knowing what scale is, you can easily measure the distance on the map or in the drawing with the help of a ruler and calculate the desired distance in reality.
Comments
To leave a comment
Arithmetic
Terms: Arithmetic