Lecture
You can always completely divide one number by another. In the examples for division, there may be a remainder. Such a division is called division with remainder .
Division with remainder is the division of one natural number by another, for which the remainder is not equal to zero.
If, when dividing natural numbers, the remainder is zero, then it is said that the dividend is divisible by a divisor without a remainder, or, in other words, completely divisible.
The division with the remainder is written as:
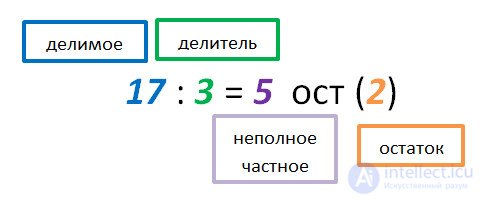
An example is read as follows:
17 divided by 3 is 5 and the balance is 2.The procedure for solving examples of division with the remainder.
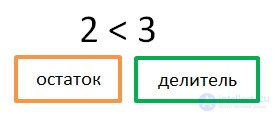
When dividing with the remainder, the remainder should always be less than the divisor.
If it turns out that the remainder is greater than the divisor, then you have incorrectly found the largest number that is divided by the divisor without a remainder.
When solving more complex examples, it is not always easy to find the largest number from paragraph 1. Sometimes, for this, it is necessary to perform additional calculations in a bar. Let's show it by example.
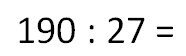
By the method of selection we find how much it is necessary to multiply 27 to get the nearest number to 190.
Let's try to multiply by 6.

Calculate the remainder and compare it with the divisor.
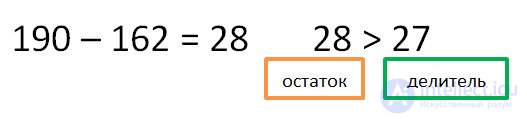
The remainder is greater than the divisor. This means that 6 as a multiplier does not suit us. Let's try to multiply the divisor by 7.
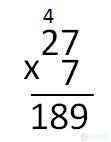
Again calculate and compare the remainder with the divisor.

The remainder is less than the divisor. So the example is solved correctly. We write the answer.
190: 27 = 7 east (1)
Comments
To leave a comment
Arithmetic
Terms: Arithmetic