Lecture
Using the concept of the modulus of a number, we formulate the rules for multiplying positive and negative numbers .
The first case you may encounter is the multiplication of numbers with the same signs.
To multiply two numbers with the same signs you need :
Examples of multiplying negative and positive numbers.
The second possible case is the multiplication of numbers with different signs.
To multiply two numbers with different signs, you need :
Examples of multiplying negative and positive numbers.
Remembering the multiplication rule is easy. This rule is the same as the rule for opening parentheses.
Two negatives make an affirmative,
Plus a minus gives a minus.
| + • (+) = + | + • (-) = - |
| - • (-) = + | - • (+) = - |
In the "long" examples, in which there is only an action of multiplication, the sign of the work can be determined by the number of negative factors.
With an even number of negative factors, the result will be positive, and with an odd number - negative.
Example.
(- 6) • (- 3) • (- 4) • (- 2) • 12 • (- 1) =In the example, five negative factors. Hence, the sign of the result will be "minus".
Now we calculate the product of the modules, not paying attention to the signs.
6 • 3 • 4 • 2 • 12 • 1 = 1728The end result of multiplying the original numbers will be:
(- 6) • (- 3) • (- 4) • (- 2) • 12 • (- 1) = - 1728If among the factors there is a number zero or a positive one, then the multiplication is performed according to the known rules.
Examples:
A special role in multiplying rational numbers is played by a negative one (- 1).




When multiplied by (- 1) the number is reversed.
In alphabetic expression this property can be written:
a • (- 1) = (- 1) • a = - aWhen performing the addition, subtraction and multiplication of rational numbers together, the procedure established for positive numbers and zero is preserved.
An example of multiplying negative and positive numbers.
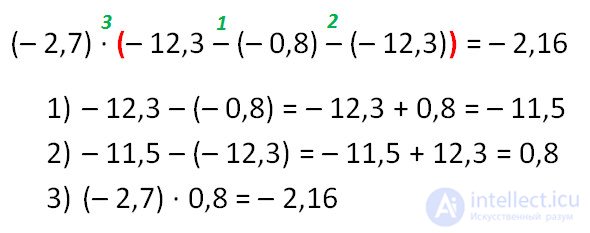
Comments
To leave a comment
Arithmetic
Terms: Arithmetic