Lecture

The location of points on the number axis allows you to visually compare the numbers between themselves.
Recall that if the coordinate straight line is shown horizontally, then positive numbers are represented by dots to the right of 0, and negative ones to the left of 0. In this case, if you mark positive numbers with dots on this straight line, then the larger one from the two numbers will correspond to the point and the smaller one is a point located on the coordinate line to the left.
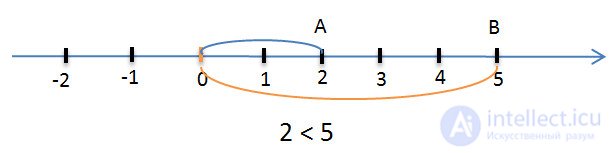
Of the two numbers on the coordinate line is greater than that which is located to the right, and less than that which is located to the left.
This means that when comparing rational numbers :
Example.
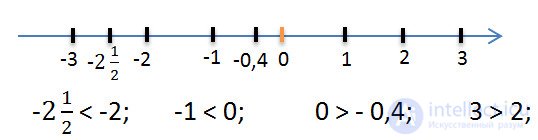
It is convenient to compare rational numbers using the concept of a module .
The larger of the two positive numbers is represented by a point located on the coordinate line to the right, that is, farther from the beginning of the reference. So this number has a larger module.
Of the two positive numbers, the one whose module is greater is greater.
When comparing two negative numbers, the larger will be located to the right, that is, closer to the beginning of the reference. This means that its modulus (the length of the segment from zero to a number) will be less.
Of the two negative numbers, the greater the modulus of which is less.
Example. Compare the numbers -6 and -12.
The point corresponding to the number -6 is closer to the beginning of reference than the point corresponding to the number -12.
| -6 | <| -12 |, therefore, -6> -12.
Comments
To leave a comment
Arithmetic
Terms: Arithmetic