Lecture
In order to find a common denominator when adding and subtracting fractions with different denominators, it is necessary to know and be able to calculate the least common multiple (LCM).
The multiple of a is the number itself divisible by the number a without a remainder.
Numbers are multiples of 8 (that is, these numbers are divided by 8 without a residue): these are numbers 16, 24, 32 ...
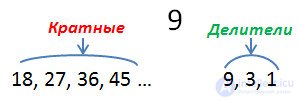
The multiples of 9: 18, 27, 36, 45 ...
The numbers that are multiples of a given number a are infinitely many, in contrast to the divisors of the same number. Dividers - a finite amount.
A common multiple of two natural numbers is a number that is divided into both these numbers completely .
The smallest common multiple (LCM) of two or more natural numbers is the smallest positive integer, which itself divides into each of these numbers.
NOC can be found and recorded in two ways.
This method is usually used for small numbers.
Example. Find the NOC 6 and 8.
K (6) = {12, 18, 24, 30, ...}This method is convenient to use to find the LCM for three or more numbers.
The number of identical factors in the decomposition of numbers can be different.
The finding of the smallest common multiple (NOC) can also be done as follows. Find the LCM (12, 16, 24).
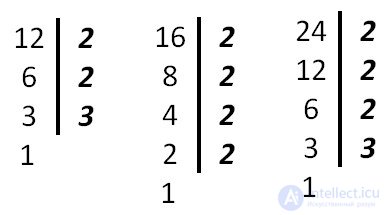 24 = 2 • 2 • 2 • 3
24 = 2 • 2 • 2 • 3 As we see from the expansion of numbers, all factors of 12 are included in the expansion of 24 (the largest of the numbers), therefore, we add only one 2 of the expansion of 16 to the LCM.
LCM (12, 16, 24) = 2 • 2 • 2 • 3 • 2 = 48
Answer: NOK (12, 16, 24) = 48
If one of the numbers is divided completely into the others, then the least common multiple of these numbers is equal to that number.
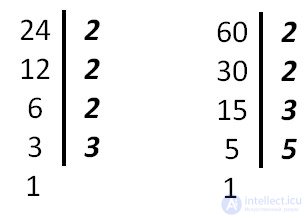
For example, LCM (60, 15) = 60
Since mutually simple numbers do not have common prime dividers, their smallest common multiple is equal to the product of these numbers.
Example.
LCM (8, 9) = 72
Comments
To leave a comment
Arithmetic
Terms: Arithmetic