Interest actions

In this lesson we will explain how to add and subtract the percentages between each other.

Addition and subtraction of interest

Percentages are added and subtracted with each other like regular numbers.

Examples:

• 1% + 37% - 25% = 38% - 25% = 13%
• 70% - (42% + 3%) = 70% - 45% = 25%

In everyday life, it is useful to know the different forms of expression of the same change in quantities formulated without percents and using percentages.

For example, a 2-fold increase means a 100% increase. Let us see why this is so.

Let x be 100%.

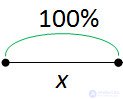
Then, having increased x 2 times, we get 2x.

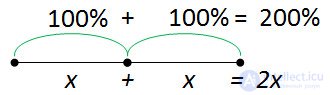
Compare the results.

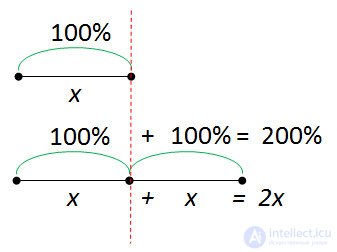
It turned out that the total number of percent is 200%. Increasing 2 times means increasing by 100% and vice versa.

Arguing in the same way, we prove that to increase by 50% means to increase 1.5 times .

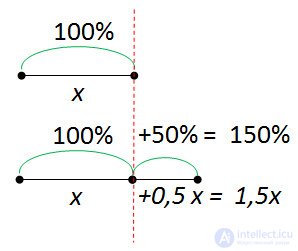
The decrease in the number can also be expressed as a percentage.

Let x be 100%.

It is known that x decreased by 80%. Find how many times decreased x.

First we find how many percent of x is left.

100% - 80% = 20%

20% left of x. We denote the remainder x by y.

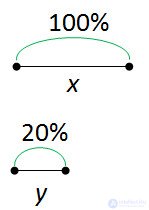
Make up the proportion. We determine by the numerical coefficient how many times x has decreased.

Thus, we have established that reducing by 80% means reducing 5 times .

Understanding the relationship between interest and “razmi”, you can easily understand what is so often said in the news and in the newspapers, citing various static data.

Some, the most commonly used phrases, it is desirable to simply remember to always understand exactly what is at stake. The list of such phrases is presented below.

The meaning of the phrases "increase and decrease by ... percent"

Increasing by 50% means increasing 1.5 times.

• 100% → 2 times
• 150% → 2.5 times
• 200% → 3 times
• 300% → 4 times

Reduce by 80%, then reduce by 5 times.

• 75% → 4 times
• 50% → 2 times
• by 25% → in ≈ 1.33 times
• 20% → 1.25 times