Lecture
Multiplication of decimal fractions occurs in three stages.
Decimal fractions are written in a column and multiplied as ordinary numbers.
We count the number of decimal places in the first decimal fraction and the second. Their number add up.
In the result obtained, we count from right to left as many digits as we got them in the paragraph above and put a comma.
Example:
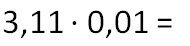
We write down decimal fractions in a column and multiply them as natural numbers, not paying attention to commas. That is, 3.11 we regard as 311, and 0.01 as 1.
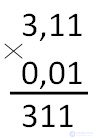
Received 311. Now we consider the number of digits (figures) after the comma in both fractions. In the first decimal there are two digits and in the second - two. Total number of digits after commas:
2 + 2 = 4
We count from right to left 4 digits (figures) of the resulting number. In the resulting result, the numbers are less than the comma must be separated. In this case, you need to assign the missing number of zeros to the left .
We lack one digit, therefore we add one zero to the left.





When multiplying any decimal fraction by 10,100,1000, etc. the decimal point is moved to the right by as many characters as zeros after the unit.
Examples:




To multiply the decimal fraction by 0.1; 0.01; 0.001; etc., it is necessary in this fraction to move the comma to the left for as many characters as zeros before the one.
We also consider zero integers!
Examples:
Comments
To leave a comment
Arithmetic
Terms: Arithmetic