Expression simplification

The properties of addition, subtraction, multiplication and division are useful in that they allow you to convert sums and products into convenient expressions for calculations. We will learn how to simplify expressions using these properties.

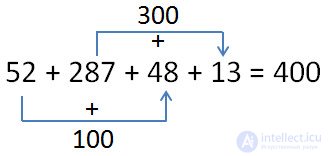
Calculate the amount:

52 + 287 + 48 + 13 =

In this expression there are numbers, the addition of which results in round numbers. Noticing this, it is easy to perform calculations orally. We use the switching law of addition.

Also, to simplify the calculation of products, one can use the commutation multiplication law.

Combination and repositioning properties are also used in simplifying letter expressions .

• 6 • a • 2 = 6 • 2 • a = 12a
• 2 • a • 4 • b = 2 • 4 • a • b = 8ab
• 5b + 8b = (5 + 8) • b = 13b
• 14y - 12y = (14 - 12) • y = 2y

The distribution law of multiplication is often used to simplify calculations.

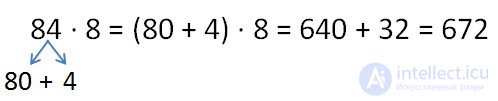
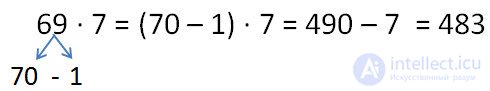
Applying the distribution property of multiplication with respect to addition or subtraction to the expression (a + b) • s and (a - b) • c, we obtain an expression that does not contain brackets. In this case, it is said that we have opened (omitted) brackets . To apply the properties, it does not matter where the “c” factor is written - before the brackets or after.

Open brackets in expressions.

• 2 (t + 8) = 2t + 16
• (3b - 5) 4 = 4 • 3b - 4 • 5 = 12b - 20

If a number is not written before the letter, then it is assumed that the number is preceded by a numerical factor of 1.

• t + 4t = (1 + 4) t = 5t

General factor out of brackets

Swap the right and left sides of the equality:

We get:

In such cases, it is said that the common factor "c" is out of the "ac + bc" brackets.

Examples of putting the common factor out of the brackets.

• 73 • 8 + 7 • 8 = (73 + 7) • 8 = 80 • 8 = 640
• 7x - x - 6 = (7 - 1) x - 6 = 6x - 6 = 6 (x - 1)