Zero to the power of zero

Zero to the power of zero, denoted by 0⁰, is a mathematical expression that is either defined as 1 or left undefined, depending on context. In algebra and combinatorics, one typically defines 0⁰ = 1. In mathematical analysis, the expression is sometimes left undefined. Computer programming languages and software also have differing ways of handling this expression.

Many widely used formulas involving natural-number exponents require 0⁰ to be defined as 1. For example, the following three interpretations of b⁰ make just as much sense for b = 0 as they do for positive integers b:

• The interpretation of b⁰ as an empty product assigns it the value 1.
• The combinatorial interpretation of b⁰ is the number of 0-tuples of elements from a b-element set; there is exactly one 0-tuple.
• The set-theoretic interpretation of b⁰ is the number of functions from the empty set to a b-element set; there is exactly one such function, namely, the empty function.^[1]

All three of these specialize to give 0⁰ = 1.

When evaluating polynomials, it is convenient to define 0⁰ as 1. A (real) polynomial is an expression of the form a₀x⁰ + ⋅⋅⋅ + a_nxⁿ, where x is an indeterminate, and the coefficients a_i are real numbers. Polynomials are added termwise, and multiplied by applying the distributive law and the usual rules for exponents. With these operations, polynomials form a ring R[x]. The multiplicative identity of R[x] is the polynomial x⁰; that is, x⁰ times any polynomial p(x) is just p(x).^[2] Also, polynomials can be evaluated by specializing x to a real number. More precisely, for any given real number r, there is a unique unital R-algebra homomorphism ev_r : R[x] → R such that ev_r(x) = r. Because ev_r is unital, ev_r(x⁰) = 1. That is, r⁰ = 1 for each real number r, including 0. The same argument applies with R replaced by any ring.^[3]

Defining 0⁰ = 1 is necessary for many polynomial identities. For example, the binomial theorem holds for x = 0 only if 0⁰ = 1.^[4]

Similarly, rings of power series require x⁰ to be defined as 1 for all specializations of x. For example, identities like and hold for x = 0 only if 0⁰ = 1.^[5]

In order for the polynomial x⁰ to define a continuous function R → R, one must define 0⁰ = 1.

In calculus, the power rule is valid for n = 1 at x = 0 only if 0⁰ = 1.

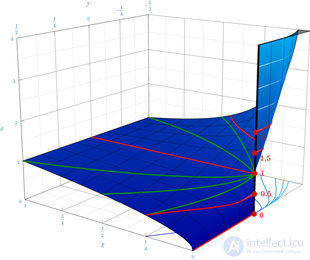
Plot of z = x^y. The red curves (with z constant) yield different limits as (x, y) approaches (0, 0). The green curves (of finite constant slope, y = ax) all yield a limit of 1.

Limits involving algebraic operations can often be evaluated by replacing subexpressions with their limits; if the resulting expression does not determine the original limit, the expression is known as an indeterminate form.^[6] The expression 0⁰ is an indeterminate form: Given real-valued functions f(t) and g(t) approaching 0 (as t approaches a real number or ±∞) with f(t) > 0, the limit of f(t)^g(t) can be any non-negative real number or +∞, or it can diverge, depending on f and g. For example, each limit below involves a function f(t)^g(t) with f(t), g(t) → 0 as t → 0⁺ (a one-sided limit), but their values are different:limt→0+tt=1,

Thus, the two-variable function x^y, though continuous on the set {(x, y) : x > 0}, cannot be extended to a continuous function on {(x, y) : x > 0} ∪ {(0, 0)}, no matter how one chooses to define 0⁰.^[7]

On the other hand, if f and g are analytic functions on an open neighborhood of a number c, then f(t)^g(t) → 1 as t approaches c from any side on which f is positive.^[8] This and more general results can be obtained by studying the limiting behavior of the function .^[9][10]

In the complex domain, the function zw may be defined for nonzero z by choosing a branch of log z and defining zw as ew log z. This does not define 0w since there is no branch of log z defined at z = 0, let alone in a neighborhood of 0.

In 1752, Euler in Introductio in analysin infinitorum wrote that a0 = 1[14] and explicitly mentioned that 00 = 1.[15] An annotation attributed[16] to Mascheroni in a 1787 edition of Euler's book Institutiones calculi differentialis[17] offered the "justification"

00=(a−a)n−n=(a−a)n(a−a)n=1

as well as another more involved justification. In the 1830s, Libri^[18][16] published several further arguments attempting to justify the claim 0⁰ = 1, though these were far from convincing, even by standards of rigor at the time.^[19]

Euler, when setting 0⁰ = 1, mentioned that consequently the values of the function 0^x take a "huge jump", from ∞ for x < 0, to 1 at x = 0, to 0 for x > 0. In 1814, Pfaff used a squeeze theorem argument to prove that x^x → 1 as x → 0⁺.^[

On the other hand, in 1821 Cauchy explained why the limit of x^y as positive numbers x and y approach 0 while being constrained by some fixed relation could be made to assume any value between 0 and ∞ by choosing the relation appropriately. He deduced that the limit of the full two-variable function x^y without a specified constraint is "indeterminate". With this justification, he listed 0⁰ along with expressions like ⁠0/0⁠ in a table of indeterminate forms.

Apparently unaware of Cauchy's work, Möbius^[8] in 1834, building on Pfaff's argument, claimed incorrectly that f(x)^g(x) → 1 whenever f(x),g(x) → 0 as x approaches a number c (presumably f is assumed positive away from c). Möbius reduced to the case c = 0, but then made the mistake of assuming that each of f and g could be expressed in the form Pxⁿ for some continuous function P not vanishing at 0 and some nonnegative integer n, which is true for analytic functions, but not in general. An anonymous commentator pointed out the unjustified step;^[ then another commentator who signed his name simply as "S" provided the explicit counterexamples (e^−1/x)^x → e⁻¹ and (e^−1/x)^2x → e⁻² as x → 0⁺ and expressed the situation by writing that "0⁰ can have many different values".

• Some authors define 0⁰ as 1 because it simplifies many theorem statements. According to Benson (1999), "The choice whether to define 0⁰ is based on convenience, not on correctness. If we refrain from defining 0⁰, then certain assertions become unnecessarily awkward. ... The consensus is to use the definition 0⁰ = 1, although there are textbooks that refrain from defining 0⁰."^[22] Knuth (1992) contends more strongly that 0⁰ "has to be 1"; he draws a distinction between the value 0⁰, which should equal 1, and the limiting form 0⁰ (an abbreviation for a limit of f(t)^g(t) where f(t), g(t) → 0), which is an indeterminate form: "Both Cauchy and Libri were right, but Libri and his defenders did not understand why truth was on their side."^[19]
• Other authors leave 0⁰ undefined because 0⁰ is an indeterminate form: f(t), g(t) → 0 does not imply f(t)^g(t) → 1.

There do not seem to be any authors assigning 0⁰ a specific value other than 1.^[22]

The IEEE 754-2008 floating-point standard is used in the design of most floating-point libraries. It recommends a number of operations for computing a power:[25]

• pown (whose exponent is an integer) treats 0⁰ as 1; see § Discrete exponents.
• pow (whose intent is to return a non-NaN result when the exponent is an integer, like pown) treats 0⁰ as 1.
• powr treats 0⁰ as NaN (Not-a-Number) due to the indeterminate form; see § Continuous exponents.

The pow variant is inspired by the pow function from C99, mainly for compatibility. It is useful mostly for languages with a single power function. The pown and powr variants have been introduced due to conflicting usage of the power functions and the different points of view (as stated above).

The C and C++ standards do not specify the result of 0⁰ (a domain error may occur). But for C, as of C99, if the normative annex F is supported, the result for real floating-point types is required to be 1 because there are significant applications for which this value is more useful than NaN^[28] (for instance, with discrete exponents); the result on complex types is not specified, even if the informative annex G is supported. The Java standard,^[29] the .NET Framework method System.Math.Pow,^[30] Julia, and Python^[31][32] also treat 0⁰ as 1. Some languages document that their exponentiation operation corresponds to the pow function from the C mathematical library; this is the case with Lua's ^ operator^[33] and Perl's ** operator^[34] (where it is explicitly mentioned that the result of 0**0 is platform-dependent).

R, SageMath, and PARI/GP^[37] evaluate x⁰ to 1. Mathematica^[38] simplifies x⁰ to 1 even if no constraints are placed on x; however, if 0⁰ is entered directly, it is treated as an error or indeterminate. Mathematica^[ and PARI/GP further distinguish between integer and floating-point values: If the exponent is a zero of integer type, they return a 1 of the type of the base; exponentiation with a floating-point exponent of value zero is treated as undefined, indeterminate or error.

See also

• Zero to the power of zero
• Indeterminate form
• Pentation
• What is the power of the number? Exposure to the power of the negative number? Procedure in the examples with degrees