Lecture
When subtracting fractions , as with the addition, there may be several cases.
When subtracting fractions with the same denominators, the numerator of the deductible (second fraction) is taken away from the numerator of the reduced (the first fraction), and the denominator is left unchanged.
Example.
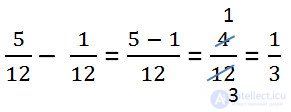
Before you write the final answer, check whether the resulting fraction can not be reduced.
In literal form, the rule of subtracting fractions with the same denominators is written as:
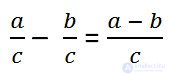
When you need to subtract the correct fraction from the unit, the unit is represented as an irregular fraction, the denominator of which is equal to the denominator of the fraction to be subtracted.
Example.
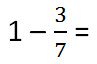
The denominator of the fraction to be subtracted is 7, which means that the unit is represented as an irregular fraction of 7/7 and is subtracted according to the rule of subtracting fractions with the same denominators.
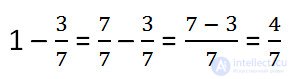
In order to subtract from a whole number the correct fraction, you need to represent this natural number as a mixed number.
To do this, we occupy a unit in the natural number and represent it in the form of an irregular fraction, the denominator of which is equal to the denominator of the fraction to be subtracted.
Example.
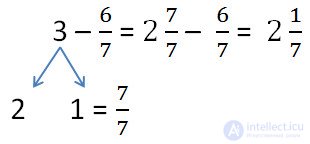
In the example, we replaced the unit with an irregular fraction of 7/7 and, instead of 3, recorded a mixed number and took the fraction from the fractional part.
When subtracting mixed numbers, the integer part is subtracted separately from the integer part, and the fractional part is subtracted from the fractional part.
When such calculations may occur different cases.
Fractional parts have the same denominators and the numerator of the fractional part of the reduced part (from which we subtract) is greater than or equal to the numerator of the fractional part of the deductible (what is subtracted).
Example.
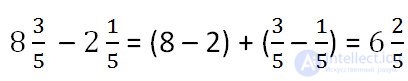
Fractional parts have different denominators.
In this case, you first need to bring the fractional parts to a common denominator, and then subtract the whole part from the whole part, and the fractional part from the fractional part.
Example.
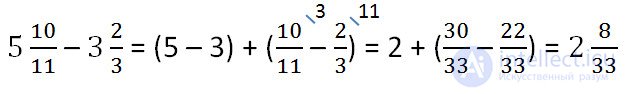
The fractional part of the reduced fractional part of the deductible.
Example.
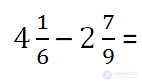
Since fractional parts have different denominators, as in the second case, we first give ordinary fractions to a common denominator.
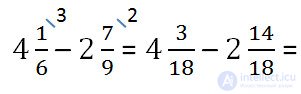
The numerator of the fractional part is decremented less than the numerator of the fractional part of the deductible.
3 <14Therefore, remembering the subtraction of the correct fraction from an integer, we take the unit from the integer part and represent this unit as an improper fraction with the same denominator and numerator equal to 18.
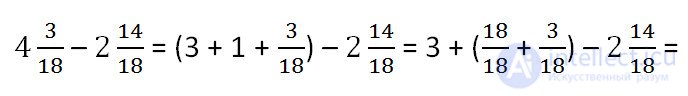
Add the resulting irregular fraction of 18/18 and the fractional part of the reduced and get:
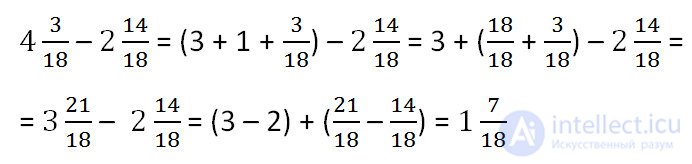
All considered cases can be described using the rules of subtraction of mixed numbers .
Comments
To leave a comment
Arithmetic
Terms: Arithmetic