Lecture
In order to solve problems on solutions and concentration , it is necessary to clearly understand what is called the concentration of the solution.
The concentration of the solution is the part that makes up the mass of the solute from the mass of the whole solution.
A kilogram of salt was dissolved in 9 liters of water. What is the concentration of the resulting solution ? (The mass of 1 l of water is 1 kg)
Using the definition of concentration given above, we solve the problem as follows.
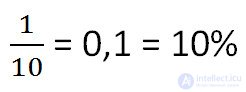
Answer: 10% is the concentration of the solution.
Now we solve the inverse problem.
No. 353 (2)How much salt will be obtained by evaporation of 375 grams of a 12% solution?
To find the mass of evaporated salt from the solution, multiply the total mass of the solution by the percentage of concentration. Do not forget to pre-convert the percentage in decimal.
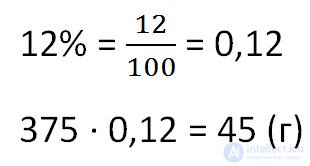
Answer: 45 grams of salt.
In a solution of 40% salt. If you add 120 grams of salt, then the percentage of salt will be equal to 70. How many grams of salt was originally in solution?
To compose a proportion, we denote by x the initial mass of salt in the solution, and by y the mass of water in the solution. Since the salt concentration in the initial solution is 40%, respectively, the water is
100% - 40% = 60%
Graphically, the conditions of the problem.
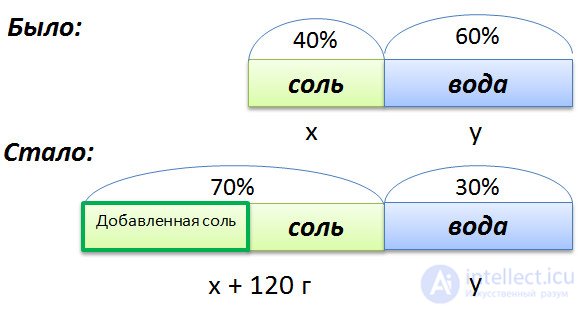
We make up the proportion that binds these quantities before adding salt.
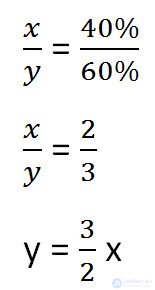
To solve the problem, we need to determine which of the unknowns (x or y) remains unchanged after adding salt.
This value is the mass of water in the solution (y).
Express it, given the changes in the solution after adding salt.
We will make a proportion similar to the previous one, but taking into account the changes that occurred after adding salt.
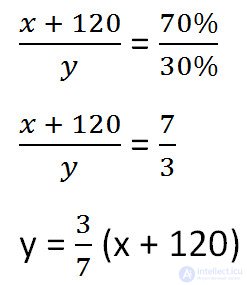
Since the mass of water remained unchanged after adding salt, we equate its values before and after adding salt and solve the equation.
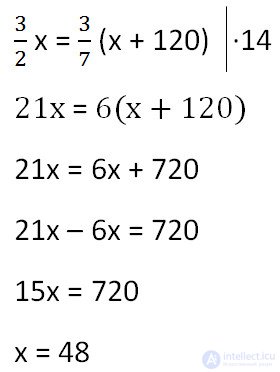
Answer: 48 g is the mass of salt in the initial solution.
Comments
To leave a comment
Arithmetic
Terms: Arithmetic