Lecture
In mathematics, tetration (or hyper-4) is an operation based on iterated, or repeated, exponentiation. There is no standard notation for tetration, though Knuth's up arrow notation ↑↑
and the left-exponent xb are common.
Under the definition as repeated exponentiation, 
means 
, where n copies of a are iterated via exponentiation, right-to-left, i.e. the application of exponentiation n−1
times. n is called the "height" of the function, while a is called the "base," analogous to exponentiation. It would be read as "the nth tetration of a".
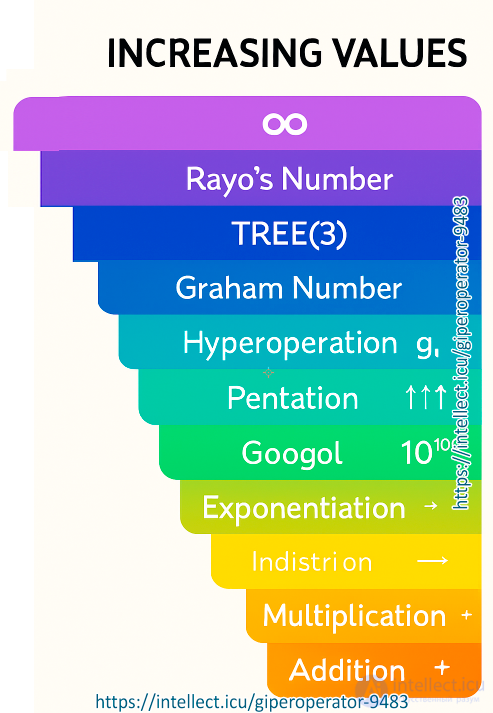
It is the next hyperoperation after exponentiation, but before pentation. The word was coined by Reuben Louis Goodstein from tetra- (four) and iteration.
Tetration is also defined recursively as
allowing for attempts to extend tetration to non-natural numbers such as real, complex, and ordinal numbers.
The two inverses of tetration are called super-root and super-logarithm, analogous to the nth root and the logarithmic functions. None of the three functions are elementary.
Tetration is used for the notation of very large numbers.
The first four hyperoperations are shown here, with tetration being considered the fourth in the series. The unary operation succession, defined as 
, is considered to be the zeroth operation.
n copies of 1 added to a combined by succession.
n copies of a combined by addition.
n copies of a combined by multiplication.
n copies of a combined by exponentiation, right-to-left.Importantly, nested exponents are interpreted from the top down: abc
means a(bc)
and not (ab)c.
Succession, 
, is the most basic operation; while addition (a+n
) is a primary operation, for addition of natural numbers it can be thought of as a chained succession of n
successors of a
; multiplication (a×n
) is also a primary operation, though for natural numbers it can analogously be thought of as a chained addition involving n numbers of a. Exponentiation can be thought of as a chained multiplication involving n numbers of a and tetration (na
) as a chained power involving n numbers a. Each of the operations above are defined by iterating the previous one;[1] however, unlike the operations before it, tetration is not an elementary function.
The parameter a is referred to as the base, while the parameter n may be referred to as the height. In the original definition of tetration, the height parameter must be a natural number; for instance, it would be illogical to say "three raised to itself negative five times" or "four raised to itself one half of a time." However, just as addition, multiplication, and exponentiation can be defined in ways that allow for extensions to real and complex numbers, several attempts have been made to generalize tetration to negative numbers, real numbers, and complex numbers. One such way for doing so is using a recursive definition for tetration; for any positive real a>0
and non-negative integer n≥0
, we can define na
recursively as:[1]
The recursive definition is equivalent to repeated exponentiation for natural heights; however, this definition allows for extensions to the other heights such as 0a
, −1a
, and ia
as well – many of these extensions are areas of active research.
There are many terms for tetration, each of which has some logic behind it, but some have not become commonly used for one reason or another. Here is a comparison of each term with its rationale and counter-rationale.
. Exponentiation is easily misconstrued: note that the operation of raising to a power is right-associative (see below). Tetration is iterated exponentiation (call this right-associative operation ^), starting from the top right side of the expression with an instance a^a (call this value c). Exponentiating the next leftward a (call this the 'next base' b), is to work leftward after obtaining the new value b^c. Working to the left, use the next a to the left, as the base b, and evaluate the new b^c. 'Descend down the tower' in turn, with the new value for c on the next downward step.Owing in part to some shared terminology and similar notational symbolism, tetration is often confused with closely related functions and expressions. Here are a few related terms:
| Terminology | Form |
|---|---|
| Tetration |  |
| Iterated exponentials |  |
| Nested exponentials (also towers) |  |
| Infinite exponentials (also towers) |  |
In the first two expressions a is the base, and the number of times a appears is the height (add one for x). In the third expression, n is the height, but each of the bases is different.
Care must be taken when referring to iterated exponentials, as it is common to call expressions of this form iterated exponentiation, which is ambiguous, as this can either mean iterated powers or iterated exponentials.
There are many different notation styles that can be used to express tetration. Some notations can also be used to describe other hyperoperations, while some are limited to tetration and have no immediate extension.
| Name | Form | Description |
|---|---|---|
| Rudy Rucker notation | na |
Used by Maurer [1901] and Goodstein [1947]; Rudy Rucker's book Infinity and the Mind popularized the notation.[nb 1] |
| Knuth's up-arrow notation |  |
Allows extension by putting more arrows, or, even more powerfully, an indexed arrow. |
| Conway chained arrow notation |  |
Allows extension by increasing the number 2 (equivalent with the extensions above), but also, even more powerfully, by extending the chain. |
| Ackermann function |  |
Allows the special case a=2 to be written in terms of the Ackermann function. |
| Iterated exponential notation |  |
Allows simple extension to iterated exponentials from initial values other than 1. |
| Hooshmand notations[6] | uxpanan |
Used by M. H. Hooshmand [2006]. |
| Hyperoperation notations |  |
Allows extension by increasing the number 4; this gives the family of hyperoperations. |
| Double caret notation | a^^n | Since the up-arrow is used identically to the caret (^), tetration may be written as (^^); convenient for ASCII. |
One notation above uses iterated exponential notation; this is defined in general as follows:
with n as.
There are not as many notations for iterated exponentials, but here are a few:
| Name | Form | Description |
|---|---|---|
| Standard notation |  |
Euler coined the notation  , and iteration notation fn(x) has been around about as long. |
| Knuth's up-arrow notation |  |
Allows for super-powers and super-exponential function by increasing the number of arrows; used in the article on large numbers. |
| Text notation | exp_a^n(x) | Based on standard notation; convenient for ASCII. |
| J Notation | x^^:(n-1)x | Repeats the exponentiation. See J (programming language)[7] |
| Infinity barrier notation |  |
Jonathan Bowers coined this,[8] and it can be extended to higher hyper-operations |
Because of the extremely fast growth of tetration, most values in the following table are too large to write in scientific notation. In these cases, iterated exponential notation is used to express them in base 10. The values containing a decimal point are approximate.
x |
2x |
3x |
4x |
5x |
6x |
7x |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 4 (22) | 16 (24) | 65,536 (216) | 2.00353 × 1019,728 | exp103(4.29508) |
exp104(4.29508) (10106.03123×1019,727) |
| 3 | 27 (33) | 7,625,597,484,987 (327) | ) |
exp104(1.09902) |
 |
) |
| 4 | 256 (44) | 1.34078 × 10154 (4256) | exp103(2.18726) |
exp104(2.18726) |
exp105(2.18726) |
exp106(2.18726) |
| 5 | 3,125 (55) | 1.91101 × 102,184 (53,125) | exp103(3.33928) (101.33574×102,184) |
 |
exp105(3.33928) |
exp106(3.33928) |
| 6 | 46,656 (66) | 2.65912 × 1036,305 (646,656) | exp103(4.55997) (102.0692×1036,305) |
exp104(4.55997) |
exp105(4.55997) |
7) |
| 7 | 823,543 (77) | 3.75982 × 10695,974 (7823,543) | exp103(5.84259) (3.17742 × 10695,974 digits) |
exp104(5.84259) |
exp105(5.84259) |
exp106(5.84259) |
| 8 | 16,777,216 (88) | 6.01452 × 1015,151,335 | exp103(7.18045) (5.43165 × 1015,151,335 digits) |
exp104(7.18045) |
exp105(7.18045) |
exp106(7.18045) |
| 9 | 387,420,489 (99) | 4.28125 × 10369,693,099 | exp103(8.56784) (4.08535 × 10369,693,099 digits) |
exp104(8.56784) |
exp105(8.56784) |
exp106(8.56784) |
| 10 | 10,000,000,000 (1010) | 1010,000,000,000 | exp103(10) (1010,000,000,000 + 1 digits) |
exp104(10) |
exp105(10) |
exp106(10) |
Remark: If x does not differ from 10 by orders of magnitude, then for all 
. For example, m=4
in the above table, and the difference is even smaller for the following rows.
Tetration can be extended in two different ways; in the equation na
, both the base a and the height n can be generalized using the definition and properties of tetration. Although the base and the height can be extended beyond the non-negative integers to different domains, including n0
, complex functions such as ni
, and heights of infinite n, the more limited properties of tetration reduce the ability to extend tetration.
In mathematics, pentation (or hyper-5) is the fifth hyperoperation. Pentation is defined to be repeated tetration, similarly to how tetration is repeated exponentiation, exponentiation is repeated multiplication, and multiplication is repeated addition. The concept of "pentation" was named by English mathematician Reuben Goodstein in 1947, when he came up with the naming scheme for hyperoperations.
The number a pentated to the number b is defined as a tetrated to itself b - 1 times. This may variously be denoted as 
, 
, 
, 
, or ba
, depending on one's choice of notation.
For example, 2 pentated to the 2 is 2 tetrated to the 2, or 2 raised to the power of 2, which is 22=4
. As another example, 2 pentated to the 3 is 2 tetrated to the result of 2 tetrated to the 2. Since 2 tetrated to the 2 is 4, 2 pentated to the 3 is 2 tetrated to the 4, which is 
.
Based on this definition, pentation is only defined when a and b are both positive integers.
Pentation is the next hyperoperation (infinite sequence of arithmetic operations) after tetration and before hexation. It is defined as iterated (repeated) tetration (assuming right-associativity). This is similar to as tetration is iterated right-associative exponentiation.[1] It is a binary operation defined with two numbers a and b, where a is tetrated to itself b − 1 times.
The type of hyperoperation is typically denoted by a number in brackets, []. For instance, using hyperoperation notation for pentation and tetration, 
means tetrating 2 to itself 2 times, or 
. This can then be reduced to .
The word "pentation" was coined by Reuben Goodstein in 1947 from the roots penta- (five) and iteration. It is part of his general naming scheme for hyperoperations.[2]
There is little consensus on the notation for pentation; as such, there are many different ways to write the operation. However, some are more used than others, and some have clear advantages or disadvantages compared to others.
. In this format, a[3]b
may be interpreted as the result of repeatedly applying the function x↦a[2]x
, for b
repetitions, starting from the number 1. Analogously, a[4]b
, tetration, represents the value obtained by repeatedly applying the function x↦a[3]x
, for b repetitions, starting from the number 1, and the pentation a[5]b represents the value obtained by repeatedly applying the function x↦a[4]x
, for b repetitions, starting from the number 1.[3][4] This will be the notation used in the rest of the article. is represented as a↑↑↑b or a↑3b. In this notation, a↑b
represents the exponentiation function ab
and a↑↑b
represents tetration. The operation can be easily adapted for hexation by adding another arrow.
.[5], though this is not extensible to higher hyperoperations.[6]The values of the pentation function may also be obtained from the values in the fourth row of the table of values of a variant of the Ackermann function: if A(n,m)
is defined by the Ackermann recurrence A(m−1,A(m,n−1))
with the initial conditions A(1,n)=an
, then a 
.[7]
As tetration, its base operation, has not been extended to non-integer heights, pentation a[5]b is currently only defined for integer values of a and b where a > 0 and b ≥ −2, and a few other integer values which may be uniquely defined. As with all hyperoperations of order 3 (exponentiation) and higher, pentation has the following trivial cases (identities) which holds for all values of a and b within its domain:
Additionally, we can also introduce the following defining relations:
Other than the trivial cases shown above, pentation generates extremely large numbers very quickly. As a result, there are only a few non-trivial cases that produce numbers that can be written in conventional notation, which are all listed below.
Some of these numbers are written in power tower notation due to their extreme size. Note that 
.
.
(a number with over 10153 digits)
(a number with more than 10102184 digits)
Comments
To leave a comment
Algebra
Terms: Algebra