When adding fractions can occur different cases.
The addition of fractions with the same denominators
Such a case is the simplest. When adding fractions with equal denominators, the numerators are added, and the denominator is left the same .
Example.
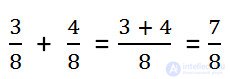
With letters, this addition rule can be written as:
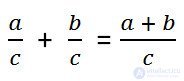
Writing the answer, check whether the resulting fraction is reduced.
Add fractions with different denominators
To add fractions with different denominators, you need to use the following rules.
- Bring these fractions to the lowest common denominator (NOR) . To do this, find the smallest common multiple of the denominators.
Example. Add fractions.
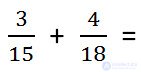
How to find a common denominator
Find the LCM (15, 18).

LCM (15, 18) = 3 • 2 • 3 • 5 = 90
- Find the extra factors for each fraction. For this, the lowest common denominator (LCM from paragraph 1) is divided in turn by the denominator of each fraction. The resulting numbers will be additional multipliers for each of the fractions. The multipliers are written over the numerator of the fraction on the right above.
90: 15 = 6 - additional factor for fraction 3/15.
90: 18 = 5 - additional factor for the fraction 4/18.
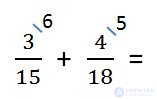
- The numerator and denominator of each fraction is multiplied by its additional factor, using the basic property of the fraction. After multiplying in the denominators of both fractions, we should get the lowest common denominator. Then we add fractions as fractions with identical denominators.

- Check the resulting fraction.
- If the result is an improper fraction, the result is written as a mixed number. Check out our fraction. 38 <90 We have the right fraction.
- If the result is reduced fraction, you must perform a reduction.
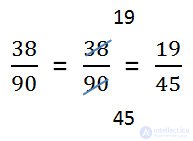
- Once again, the whole example.
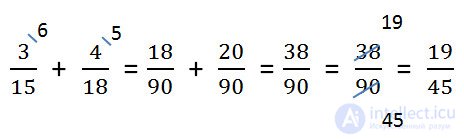
Addition of mixed numbers
The combination and relocation properties of addition allow the addition of mixed numbers to the addition of their integral parts and the addition of their fractional parts.
To add mixed numbers you need.
- Separately fold their whole parts.
Example.
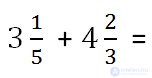
Fold the whole parts.
3 + 4 = 7
- Separately fold the fractional parts.
If the fractional parts denominators are different, then first we bring them to a common denominator, and then add.
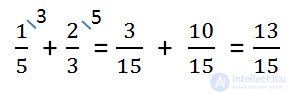
- Add the results from points 1 and 2.
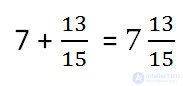
- If the addition of fractional parts turned out to be an incorrect fraction, then you need to select the whole part from this fraction and add to the whole part obtained in paragraph 1.
Another example of the addition of fractions .
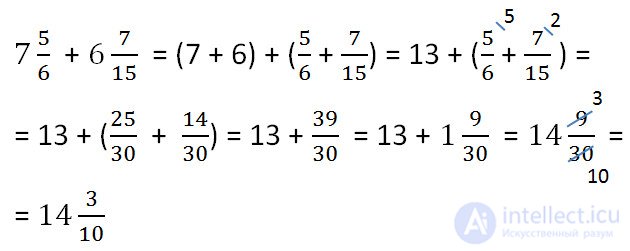
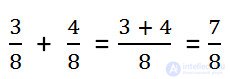
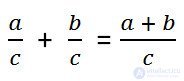
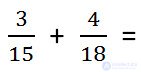
 LCM (15, 18) = 3 • 2 • 3 • 5 = 90
LCM (15, 18) = 3 • 2 • 3 • 5 = 90
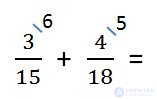

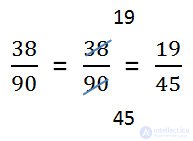
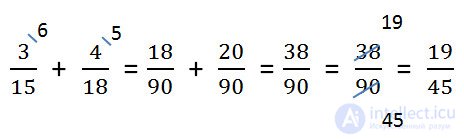
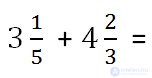
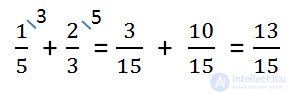
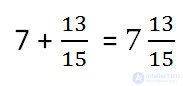
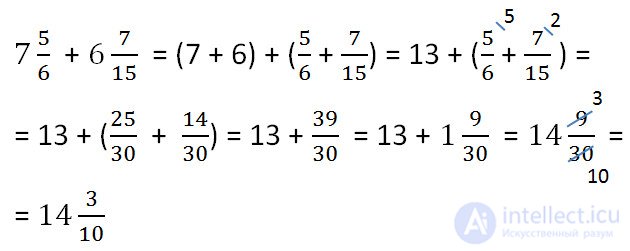
Comments
To leave a comment
Arithmetic
Terms: Arithmetic