Lecture
As well as natural numbers, ordinary fractions can be compared.
Consider two unequal fractions on the number axis. A smaller fraction will be located to the left, and a larger fraction to the right.
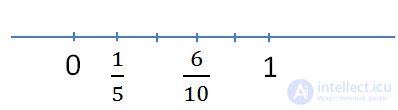
Equal fractions correspond to the same point on the number axis.
The figure clearly shows that 1/5 <6/10. But it is not necessary to use the number axis to compare fractions .
Of the two fractions with the same denominators, the one with the numerator is greater.
Example. Compare 1/5 and 4/5.
In both fractions the same denominator is 5.
In the first fraction, the numerator is 1 and it is less than the numerator of the second fraction, which is 4.
Therefore, the first fraction (1/5) is less than the second (4/5).
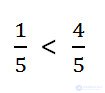
Of the two fractions with the same numerators, the one with the smaller denominator is greater.
Example. Compare 1/2 and 1/8. Answer:
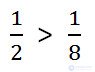
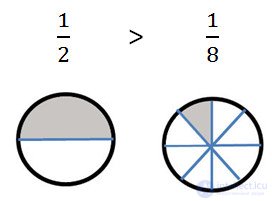
The rule above is easier to understand if you imagine that you have pieces of cake in your hands. In the first case, the cake was divided into 2 parts (the denominator of the fraction is 2), and you have half the cake in your hands, and in the second, the cake was divided into 8 parts, and you have a small piece of cake in your hands.
To compare fractions with different denominators , you need to bring the fraction to a common denominator.
After reduction of fractions to a common denominator, fractions are compared by the rule of comparison of fractions with the same denominators.
Example. Compare 2/7 and 1/14.
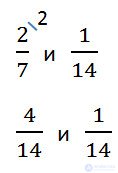
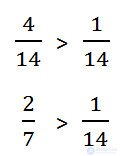
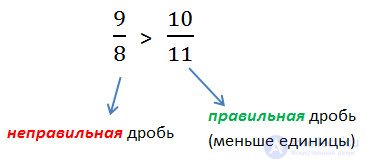
Any improper fraction is greater than any improper fraction.
This is because the wrong fraction is always greater than or equal to 1, and the correct fraction is always less than 1.
Comments
To leave a comment
Arithmetic
Terms: Arithmetic