Lecture
How to perform the division of negative numbers is easy to understand, remembering that division is the opposite of multiplication.
If a and b are positive numbers, then divide the number a by the number b, then find a number c, which, when multiplied by b, gives the number a.
This definition of division is valid for any rational numbers if the divisors are non-zero.
Therefore, for example, to divide the number (- 15) by the number 5 means to find such a number, which when multiplied by the number 5 gives the number (- 15). This number will be (- 3), since
(- 3) • 5 = - 15Examples of the division of rational numbers .
It is clear from the examples that the quotient of two numbers with the same signs is a positive number (examples 1, 2), and the quotient of two numbers with different signs is a negative number (examples 3,4).
To find the private module, you need to divide the divisible module by the divisor module.
So, to separate two numbers with the same characters , you need:
Examples of dividing numbers with the same characters:
To separate two numbers with different signs , you need:
Examples of dividing numbers with different signs:
You can also use the following table to determine the sign of the quotient.
| +: (+) = + | +: (-) = - |
| -: (-) = + | -: (+) = - |
When calculating “long” expressions, in which only multiplication and division appear, it is very convenient to use the sign rule. For example, to calculate the fraction
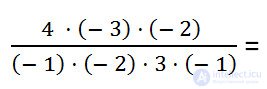
It can be noted that in the numerator there are 2 minus signs, which, when multiplied, will give a plus. Also in the denominator are three minus signs, which, when multiplied, will give a minus. Therefore, in the end, the result will be with a minus sign.
The reduction of the fraction (further actions with modules of numbers) is performed as before:
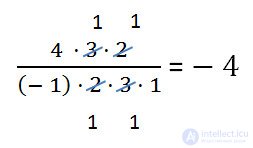
The quotient from dividing zero by a non-zero number is zero.
0: a = 0, a ≠ 0
It is IMPOSSIBLE to divide by zero!
All previously known rules of dividing by one act on the set of rational numbers.
Dependencies between the results of multiplication and division, known for positive numbers, are also preserved for all rational numbers (except the number zero):
These dependences are used to find the unknown multiplier, the dividend and the divisor (when solving equations), as well as to check the results of multiplication and division.
An example of finding the unknown.
x • (- 5) = 10Divide the number (- 5) by 6 and the number 5 by (- 6).
We remind you that the trait in the record of an ordinary fraction is the same division sign, and we write down the quotient of each of these actions in the form of a negative fraction.
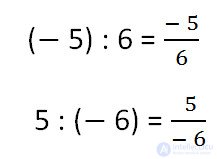
Thus, the minus sign in a fraction may be:
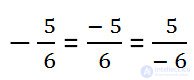
When recording negative fractions, the minus sign can be placed in front of the fraction, transferred from the numerator to the denominator or from the denominator to the numerator.
This is often used when performing fractions, making it easier to calculate.
Example. Please note that after making a minus sign in front of the bracket, we subtract the smaller one from the larger module by the rules of addition of numbers with different signs.
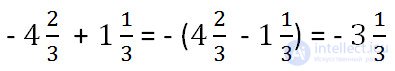
Example.
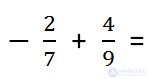
Using the described property of transfer of a sign in fractions, you can act without figuring out which of the given fractional numbers is greater.
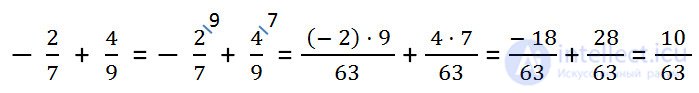
Comments
To leave a comment
Arithmetic
Terms: Arithmetic