The absolute value of a number

Denote on the coordinate straight line two points that correspond to the numbers -4 and 2.

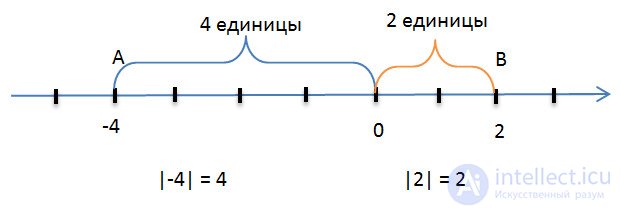
Point A, corresponding to the number -4, is at a distance of 4 unit segments from point 0 (the origin), that is, the length of the segment OA is 4 units.

The number 4 (the length of the segment OA) is called the modulus of the number -4.

Denote the modulus of a number as follows: | -4 | = 4

Read the characters above as follows: “the modulus of the number minus four is four”.

Point B, corresponding to the number +2, is at a distance of two unit segments from the origin, that is, the length of the segment OB is equal to two units.

The number 2 is called the modulus of the number +2 and is written: | +2 | = 2 or | 2 | = 2.

If we take a certain number “a” and draw it as a point A on the coordinate line, then the distance from point A to the beginning of reference (in other words, the length of the segment OA) will be called the modulus of the number “a”.

Since the distance (the length of the segment) can only be expressed as a positive number or zero, one can say that the modulus of a number cannot be negative.

We will write down the properties of the module using letter expressions, having considered all possible cases.

1. The modulus of a positive number is the number itself.
   | a | = a, if a> 0;
2. The modulus of a negative number is the opposite number.
   | -a | = a, if a <0;
3. The zero module is zero.
   | 0 | = 0 if a = 0;
4. Opposite numbers have equal modules.
   | -a | = | a |;

Examples of modules of rational numbers:

• | -4,8 | = 4.8
• | 0 | = 0
• | -3/8 | = | 3/8 |