Cell Decomposition Techniques

The first approach to planning a path uses cell decomposition ; in other words, in this method, free space is decomposed into a finite number of continuous sections, called cells . These sections have the important property that the task of planning a path within one section can be solved by simple means (for example, in the form of movement in a straight line). Thus, the task of planning a path is transformed into a task of searching in a discrete graph.

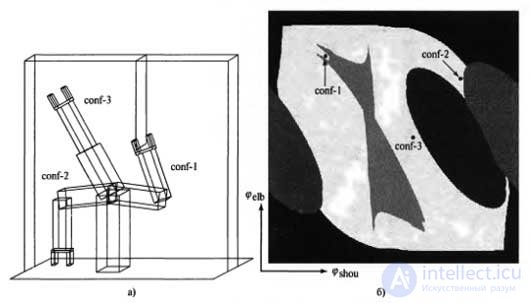
Three robot configurations shown in the workspace and configuration space

The simplest cell decomposition is a grid with uniform pitch. Figure a) shows the decomposition of space using a square grid and the optimal solution for a grid with these dimensions. In addition, this figure uses shading in the form of gray gradations to denote the cost of each grid cell, i.e. the cost of the shortest path from this cell to the goal. Figure b) shows the corresponding trajectory of the manipulator in the workspace.

This decomposition has the advantage of providing an extremely simple implementation, but it is also characterized by two limitations. First, it can be used only for configuration spaces with a small number of dimensions, since the number of grid cells grows exponentially depending on d , i.e. on the number of measurements. Secondly, a problem arises due to the fact that some cells are "mixed", i.e. do not belong completely to either free or occupied space. The path found as a solution that includes such a cell may not correspond to the actual solution, due to the fact that there will be no way to intersect the cell in the desired direction in a straight line. As a result, the path planning procedure becomes controversial. On the other hand, if we insist that only completely free cells are used, the planning procedure will become incomplete, due to the fact that there may be cases in which the only possible paths to the target lie through mixed cells, especially if the cell size is comparable with the sizes of passes and gaps in the considered space.

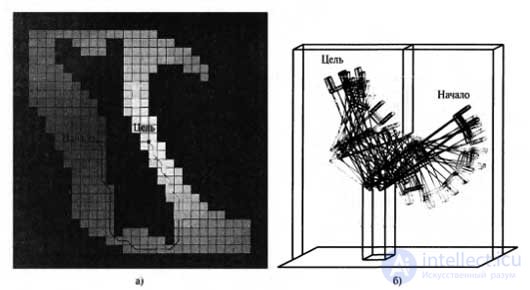
An example of using the cell decomposition method: the cost function and the path found by approximating the space of configurations in the form of grid cells (a); the same path, visually represented by the coordinates of the workspace (b). Notice how the robot bends its elbow to prevent collision with a vertical obstacle.

There are two ways to improve the cell decomposition method to correct these shortcomings. The first of these is that further separation of mixed cells is allowed, possibly using cells half the size of the original size. Such an operation can continue recursively until a path is found that completely passes through free cells. (Of course, this method can be used only if it is possible to determine whether this particular cell is mixed, and this operation is simple only if the boundaries of the configuration space are determined using relatively simple mathematical descriptions.) This method is complete, provided that restrictions are set on the value of the smallest passage through which the desired path must pass. Although the main part of the computational effort focuses on the most complex areas in the configuration space, this method still does not allow for successful scaling and extending it to multidimensional tasks, since 2d smaller cells are created for each recursive partitioning of the cell. The second way to obtain a complete algorithm is to strictly comply with the requirement of precise decomposition of the cells of free space. This method should allow cells to take an irregular shape in those places where they meet with the boundaries of free space, but these forms still have to be "simple" in the sense that using them could easily calculate the trajectory of passage through any free cell. . To implement this method requires the use of some very complex geometric concepts, so this method will not be discussed in more detail here.

Considering the solution path shown in Figure a) , one can notice additional difficulties that need to be overcome. First, it should be noted that this path contains arbitrarily sharp angles; a robot moving with a finite speed cannot follow this path. Secondly, it is noteworthy that the path passes very close to the obstacle. Anyone who drives a car knows that a parking lot, where one millimeter of clearance is left on each side, is in fact not suitable for parking at all; for the same reason, one should prefer such solutions that are not sensitive to small errors of movement.

It is desirable to maximize the distance from the obstacles and at the same time minimize the length of the path. This goal can be achieved by introducing the concept of a potential field . The potential field is a function defined in the state space, the value of which grows in proportion to the distance to the nearest obstacle. Such a field of potentials is shown in figure a) , - the darker the color indicates the point in the configuration space, the closer it is to the obstacle. When used in a path planning problem, this potential field becomes an additional cost term in the optimization equation. Because of this, an interesting situation of finding a compromise arises. On the one hand, the robot seeks to minimize the length of the path to the target. On the other hand, he tries to stay away from obstacles, adhering to the minimum values ​​of the potential function. Assigning the corresponding weights to both targets, one can find approximately such a path, as shown in Figure b). This figure also shows the cost function derived from the combined cost function, which in this case is also computed using a iteration over costs. Obviously, the resulting path is longer, but at the same time safer.

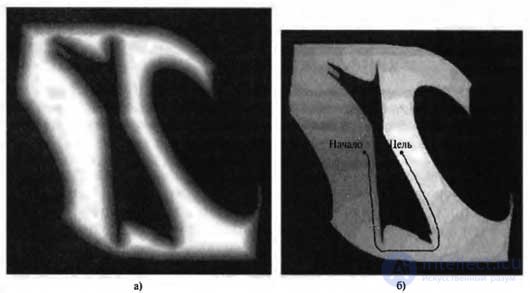
The method of using the potential field: the potential field preventing the approaching one pushes the robot away from obstacles (a); path found by simultaneously minimizing path length and potential (b)