Lecture
Two intersecting straight lines form adjacent and vertical angles. Vertical angles are equal, and adjacent angles complement each other up to 180º. The angular measure of the smaller of them is called the angle between the straight lines .
The angle between the crossed straight lines is the angle between the intersecting straight lines that are parallel to the given crossed straight lines.
In this article, we first give the definition of the angle between the crossed straight lines and give a graphic illustration. Next, we answer the question: “How to find the angle between intersecting straight lines if the coordinates of the direction vectors of these straight lines are known in a rectangular coordinate system”? In conclusion, we will practice finding the angle between intersecting straight lines when solving examples and problems.
The definition of the angle between crossed lines will be approached gradually.
First, we recall the definition of intersecting lines: two straight lines in three-dimensional space are called intersecting , if they do not lie in the same plane. From this definition it follows that the intersecting lines do not intersect, are not parallel, and, moreover, do not coincide, otherwise both of them would lie in a certain plane.
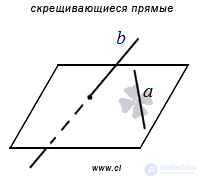
We also give auxiliary arguments.
Let two intersecting lines a and b be given in three-dimensional space. We construct the lines a 1 and b 1 so that they are parallel to the intersecting lines a and b, respectively, and pass through a certain point in the space M 1 . Thus, we obtain two intersecting straight lines a 1 and b 1 . Let the angle between intersecting straight lines a 1 and b 1 be equal to the angle 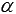 . Now we construct the lines a 2 and b 2 parallel to the intersecting lines a and b, respectively, passing through the point M 2 , which is different from the point M 1 . The angle between the intersecting straight lines a 2 and b 2 will also be equal to the angle
. Now we construct the lines a 2 and b 2 parallel to the intersecting lines a and b, respectively, passing through the point M 2 , which is different from the point M 1 . The angle between the intersecting straight lines a 2 and b 2 will also be equal to the angle  . This statement is true, since the straight lines a 1 and b 1 will coincide with the straight lines a 2 and b 2, respectively, if we perform a parallel transfer, at which point M 1 goes to point M 2 . Thus, the measure of the angle between two straight lines intersecting at a point M , respectively parallel to a given crossed straight line, does not depend on the choice of the point M.
. This statement is true, since the straight lines a 1 and b 1 will coincide with the straight lines a 2 and b 2, respectively, if we perform a parallel transfer, at which point M 1 goes to point M 2 . Thus, the measure of the angle between two straight lines intersecting at a point M , respectively parallel to a given crossed straight line, does not depend on the choice of the point M.
Now we are ready to define the angle between intersecting lines.
Definition
The angle between intersecting straight lines is the angle between two intersecting straight lines that are respectively parallel to a given crossed straight line.
It follows from the definition that the angle between the crossed straight lines will also not depend on the choice of the point M. Therefore, as a point M one can take any point belonging to one of the crossed straight lines.
We give an illustration of the definition of the angle between crossed lines.
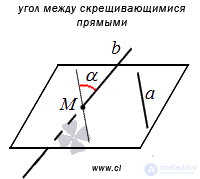
Since the angle between intersecting straight lines is determined through the angle between intersecting straight lines, finding the angle between intersecting straight lines is reduced to finding the angle between the corresponding intersecting straight lines in three-dimensional space.
Undoubtedly, the methods studied in geometry lessons in high school are suitable for finding the angle between crossed lines. That is, by completing the necessary constructions, you can associate the desired angle with any known condition from the angle, based on the equality or similarity of the figures, in some cases the cosine theorem will help, and sometimes the definition of the sine, cosine and tangent of a right-angled triangle will result.
However, it is very convenient to solve the problem of finding the angle between intersecting straight lines by the coordinate method. That is what we consider.
Let the rectangular coordinate system Oxyz be introduced in three-dimensional space (although in many problems it has to be entered independently).
We set ourselves the task: to find the angle 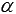 between the crossed straight lines a and b , which correspond in the rectangular coordinate system Oxyz to some equations of a straight line in space.
between the crossed straight lines a and b , which correspond in the rectangular coordinate system Oxyz to some equations of a straight line in space.
We will solve it.
Take an arbitrary point in the three-dimensional space M and assume that the straight lines a 1 and b 1 pass through it, parallel to the intersecting straight lines a and b, respectively. Then the desired angle 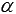 between the crossed straight lines a and b is equal to the angle between the intersecting straight lines a 1 and b 1 by definition.
between the crossed straight lines a and b is equal to the angle between the intersecting straight lines a 1 and b 1 by definition.
Thus, it remains for us to find the angle between the intersecting straight lines a 1 and b 1 . To apply the formula for finding the angle between two intersecting straight lines in space, we need to know the coordinates of the direction vectors of the straight lines a 1 and b 1 .
How can we get them? A very simple. The definition of a direct vector of a straight line allows us to state that the sets of directing vectors of parallel straight lines coincide. Therefore, as the directing vectors of the lines a 1 and b 1, we can take the direction vectors  and
and 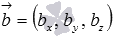 straight lines a and b respectively.
straight lines a and b respectively.
Coordinates of vectors 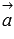 and
and 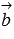 are determined either by the conditional straight lines a and b known from the condition (see the section of the coordinates of the direct vector of the straight line), or by the coordinates of the two points of the straight lines a and b known by the condition (the theory of coordinate coordinates of the vector through the points of its beginning and end can be useful here).
are determined either by the conditional straight lines a and b known from the condition (see the section of the coordinates of the direct vector of the straight line), or by the coordinates of the two points of the straight lines a and b known by the condition (the theory of coordinate coordinates of the vector through the points of its beginning and end can be useful here).
So, the angle between two crossed straight lines a and b is calculated by the formula 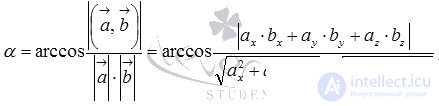 where
where  and
and 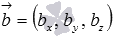 - the direction vectors of the lines a and b, respectively.
- the direction vectors of the lines a and b, respectively.
The formula for finding the cosine of the angle between the intersecting straight lines a and b is 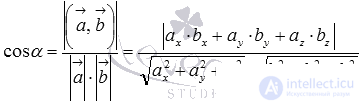 .
.
The basic trigonometric identity allows us to find the sine of the angle between the crossing lines, if the cosine is known: 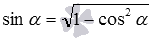 .
.
It remains to analyze the solutions of examples.
Example.
Find the angle between the crossed straight lines a and b , which are defined in the rectangular coordinate system Oxyz by the equations 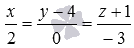 and
and 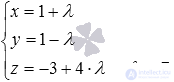 .
.
Decision.
The canonical equations of a straight line in space allow us to immediately determine the coordinates of the directing vector of this straight line - they are given by the numbers in the denominators of fractions, that is, 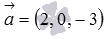 - directing vector straight
- directing vector straight 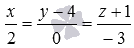 .Parametric equations of a straight line in space also make it possible to immediately write down the coordinates of the directing vector - they are equal to the coefficients before the parameter, that is,
.Parametric equations of a straight line in space also make it possible to immediately write down the coordinates of the directing vector - they are equal to the coefficients before the parameter, that is, 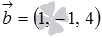 - directing vector straight
- directing vector straight 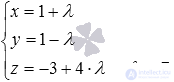 . Thus, we have all the necessary data to apply the formula, which calculates the angle between the skew lines:
. Thus, we have all the necessary data to apply the formula, which calculates the angle between the skew lines: 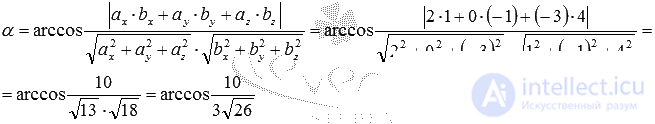
Answer:
the angle between the given crossed straight lines is 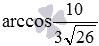 .
.
Example.
Find the sine and cosine of the angle between the intersecting lines on which the AD and BC edges lie on the ABCD pyramid, if the coordinates of its vertices are known: 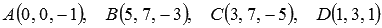 .
.
Decision.
The guiding vectors of the crossing lines AD and BC are vectors 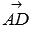 and
and 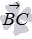 . We calculate their coordinates as the difference of the corresponding coordinates of the points of the end and the beginning of the vector:
. We calculate their coordinates as the difference of the corresponding coordinates of the points of the end and the beginning of the vector: 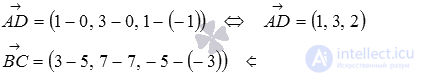
According to the formula 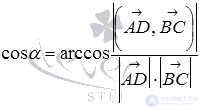 we can calculate the cosine of the angle between the indicated intersecting lines:
we can calculate the cosine of the angle between the indicated intersecting lines: 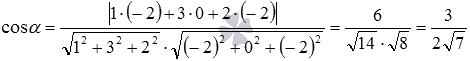
Now let's calculate the sine of the angle between the crossed lines: 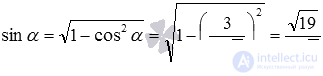
Answer:
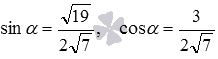
In conclusion, we consider the solution of the problem in which we need to find the angle between the intersecting straight lines, and the rectangular coordinate system has to be entered independently.
Example.
Given a rectangular parallelepiped ABCDA 1 B 1 C 1 D 1 , for which AB = 3 , AD = 2 and AA 1 = 7 units. Point E lies on the edge AA 1 and divides it in the ratio of 5 to 2 counting from point A. Find the angle between the intersecting straight lines BE and A 1 С.
Decision.
Since the edges of a rectangular parallelepiped at one vertex are mutually perpendicular, it is convenient to introduce a rectangular coordinate system, and determine the angle between the indicated intersecting straight lines by the coordinate method through the angle between the guiding vectors of these lines.
We introduce a rectangular coordinate system Oxyz as follows: let the origin of coordinates coincide with the vertex A , the axis Ox coincides with the straight line AD , the axis Oy with the straight line AB , and the axis Oz with the straight line AA 1 .
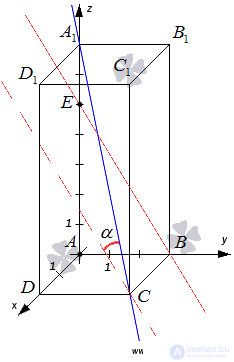
Then point B has coordinates 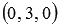 point E -
point E - 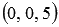 (if necessary, see the article dividing the segment in this respect), point А 1 -
(if necessary, see the article dividing the segment in this respect), point А 1 - 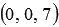 , and point C -
, and point C - 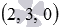 . According to the coordinates of these points, we can calculate the coordinates of vectors
. According to the coordinates of these points, we can calculate the coordinates of vectors 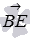 and
and 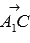 . We have
. We have 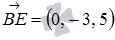 ,
, 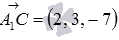 .
.
It remains to apply the formula for finding the angle between the intersecting straight lines along the coordinates of the guiding vectors: 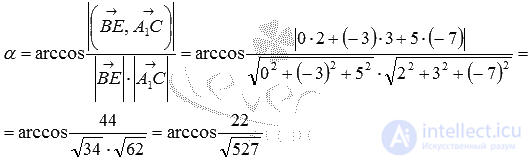
Answer:
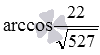
Comments
To leave a comment
Stereometry
Terms: Stereometry