Parallelepiped. Properties

Theorem

The parallelepiped opposite faces are parallel and equal.



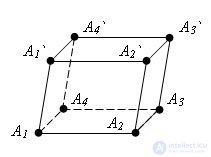Evidence

Take any two opposite faces of the parallelepiped: A1A2A2`A1` and A3A4A4`A3`. Since all the faces of the parallelepiped are parallelograms, the straight line A1A2 is parallel to straight line A4A3, and straight line A1A1` is parallel to straight line A4A4`. Therefore, the planes of the faces under consideration are parallel.
Since the faces of the parallelepiped are parallelograms, the segments A1A4, A1`A4`, A2`A3` and A2A3 are parallel and equal. Therefore, the edge A1A2A2`A1` is combined by parallel transfer along the edge A1A4 with the edge A3A4A4`A3` and, therefore, the faces are equal.
The parallelism and equality of other opposite faces of the parallelepiped is proved in the same way. The theorem is proved.