Lecture
Theorem
The angle between the planes does not depend on the choice of the cutting plane. 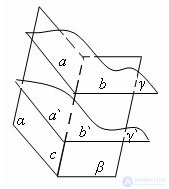
Evidence.
Suppose there are two planes α and β, which intersect along a straight line c. draw the plane γ perpendicular to the line with. Then the plane γ intersects the planes α and β along straight lines a and b, respectively. The angle between the planes α and β is equal to the angle between the straight lines a and b.
Take another cutting plane γ` perpendicular to c. Then the plane γ` intersects the planes α and β along the straight lines a` and b`, respectively.
With parallel transfer, the point of intersection of the plane γ from the straight line c goes to the point of intersection of the plane γ` from the straight line c. at the same time, by the property of parallel translation, the straight line a will turn into the straight line a`, b - into the straight line b`. hence the angles between straight lines a and b, a `and b` are equal. The theorem is proved.
This article focuses on the angle between the planes and its location. First, the definition of the angle between two planes is given and a graphic illustration is given. After that, the principle of finding the angle between two intersecting planes by the method of coordinates is analyzed, a formula is obtained that allows to calculate the angle between intersecting planes from the known coordinates of the normal vectors of these planes. In conclusion, detailed solutions of characteristic problems are shown.
In presenting the material, we will use the definitions and concepts given in the articles in the plane in space and straight in space.
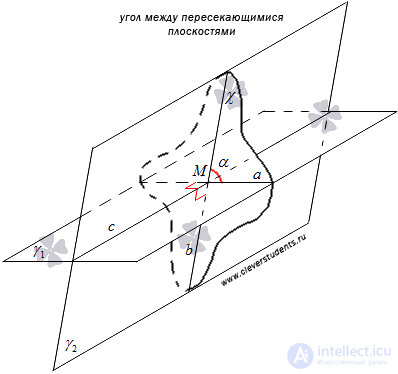
We present the arguments that will allow us to gradually approach the definition of the angle between two intersecting planes.
Let us be given two intersecting planes.  and
and  . These planes intersect in a straight line, which we denote by the letter c . Build a plane
. These planes intersect in a straight line, which we denote by the letter c . Build a plane 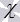 passing through the point M of the line c and perpendicular to the line c . With this plane
passing through the point M of the line c and perpendicular to the line c . With this plane 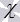 will cross the plane
will cross the plane  and
and  . Denote the line on which the planes intersect
. Denote the line on which the planes intersect  and
and 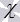 as a , and the line along which the planes intersect
as a , and the line along which the planes intersect  and
and 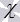 as b . Obviously, the lines a and b intersect at the point M.
as b . Obviously, the lines a and b intersect at the point M.
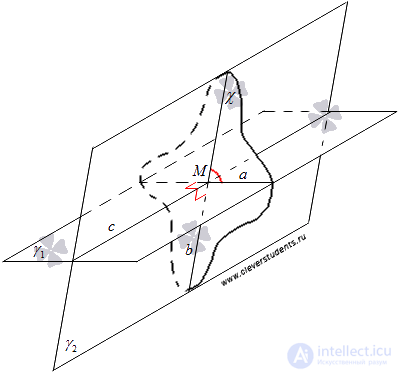
It is easy to show that the angle between the intersecting straight lines a and b does not depend on the location of the point M on the straight line c through which the plane passes 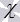 .
.
Build a plane 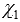 perpendicular to the line c and different from the plane
perpendicular to the line c and different from the plane 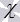 . Plane
. Plane 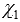 cross the planes
cross the planes  and
and  along straight lines, which we denote by a 1 and b 1, respectively.
along straight lines, which we denote by a 1 and b 1, respectively.
From the method of constructing planes 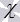 and
and 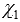 it follows that the lines a and b are perpendicular to the line c , and the lines a 1 and b 1 are perpendicular to the line c . Since the lines a and a 1 lie in the same plane
it follows that the lines a and b are perpendicular to the line c , and the lines a 1 and b 1 are perpendicular to the line c . Since the lines a and a 1 lie in the same plane  and perpendicular to c , they are parallel. Similarly, straight lines b and b 1 lie in one plane
and perpendicular to c , they are parallel. Similarly, straight lines b and b 1 lie in one plane  and perpendicular to c , therefore, they are parallel. Thus, it is possible to perform parallel transfer of the plane.
and perpendicular to c , therefore, they are parallel. Thus, it is possible to perform parallel transfer of the plane. 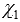 on the plane
on the plane 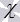 in which the straight line a 1 coincides with the straight line a , and the straight line b with the straight line b 1 . Therefore, the angle between the two intersecting straight lines a 1 and b 1 is equal to the angle between the intersecting straight lines a and b .
in which the straight line a 1 coincides with the straight line a , and the straight line b with the straight line b 1 . Therefore, the angle between the two intersecting straight lines a 1 and b 1 is equal to the angle between the intersecting straight lines a and b .
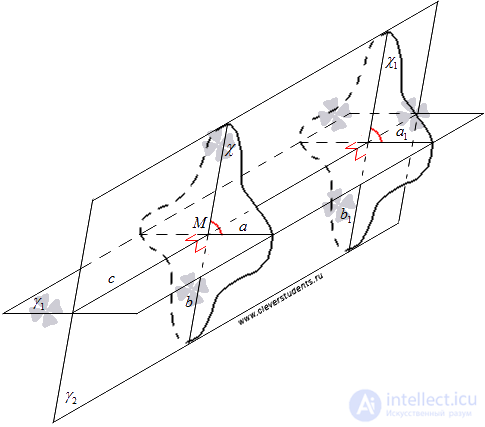
This proved that the angle between intersecting straight lines a and b lying in intersecting planes  and
and  , does not depend on the choice of the point M through which the plane passes
, does not depend on the choice of the point M through which the plane passes 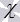 . Therefore, it is logical to take this angle as the angle between two intersecting planes.
. Therefore, it is logical to take this angle as the angle between two intersecting planes.
Now you can voice the definition of the angle between two intersecting planes  and
and  .
.
Definition
The angle between two planes intersecting in a straight line  and
and  Is the angle between two intersecting straight lines a and b , along which the planes
Is the angle between two intersecting straight lines a and b , along which the planes  and
and  intersect with the plane
intersect with the plane 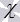 perpendicular to the line c .
perpendicular to the line c .
The definition of the angle between two planes can be given a little differently. If on a line with , on which planes intersect  and
and  , mark the point M and through it draw the lines a and b , perpendicular to the line c and lying in the planes
, mark the point M and through it draw the lines a and b , perpendicular to the line c and lying in the planes  and
and  respectively, the angle between the lines a and b is the angle between the planes
respectively, the angle between the lines a and b is the angle between the planes  and
and  . It is usually in practice that such constructions are carried out in order to obtain an angle between the planes.
. It is usually in practice that such constructions are carried out in order to obtain an angle between the planes.
Since the angle between intersecting straight lines does not exceed 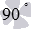 then from the voiced definition it follows that the degree measure of the angle between two intersecting planes is expressed by a real number from the interval
then from the voiced definition it follows that the degree measure of the angle between two intersecting planes is expressed by a real number from the interval 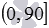 . At the same time, intersecting planes are called perpendicular if the angle between them is ninety degrees. The angle between parallel planes is either not determined at all, or is considered equal to zero.
. At the same time, intersecting planes are called perpendicular if the angle between them is ninety degrees. The angle between parallel planes is either not determined at all, or is considered equal to zero.
Usually, when finding the angle between two intersecting planes, you first have to perform additional constructions to see intersecting straight lines, the angle between which is equal to the desired angle, and then link this angle with the original data using equality signs, similarity signs, cosine theorems or definitions of sine, cosine and tangent angle. There are similar tasks in the course of high school geometry.
For example, let us give a solution to problem C2 from the Unified State Exam in mathematics for 2012 (the condition is intentionally changed, but this does not affect the principle of solution). It just needed to find the angle between two intersecting planes.
Example.
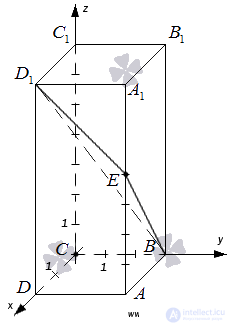
Given a rectangular parallelepiped of ABCDA 1 B 1 C 1 D 1 , in which AB = 3 , AD = 2 , AA 1 = 7 and the point E divides the side AA 1 in the ratio 4 to 3 , counting from point A. Find the angle between the ABC and BED 1 planes .
Decision.
To begin with we will make the drawing.
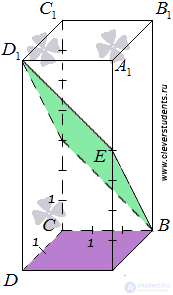
Perform additional constructions to "see" the angle between the planes.
To begin with, we define a straight line along which the planes ABC and BED 1 intersect. Point B is one of their common points. Find the second common point of these planes. Straight lines DA and D 1 E lie in one plane АDD 1 , and they are not parallel, and, therefore, intersect. On the other hand, the straight line DA lies in the plane ABC , and the straight line D 1 E - in the plane BED 1 , therefore, the intersection point of the straight lines DA and D 1 E will be a common point of the planes ABC and BED 1 . So, we continue the lines DA and D 1 E to their intersection, we denote the point of their intersection by the letter F. Then BF is the line along which the planes ABC and BED 1 intersect.
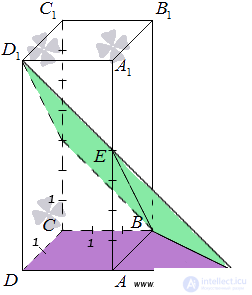
It remains to build two straight lines lying in the ABC and BED 1 planes, respectively, passing through one point on the BF straight line and perpendicular to the BF straight line - the angle between these straight lines will by definition be equal to the desired angle between the ABC and BED 1 planes. Let's do it.
Point A is the projection of point E on the plane ABC . Draw a line that intersects the BF at a right angle at the point M. Then the straight line AM is the projection of the straight line EM to the plane ABC , and by the theorem on three perpendiculars 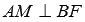 .
.
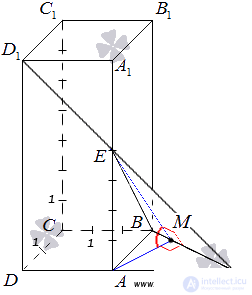
Thus, the desired angle between the planes ABC and BED 1 is equal to 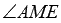 .
.
We can determine the sine, cosine or tangent of this angle (and hence the angle itself) from the right triangle AEM if we know the lengths of its two sides. From the condition it is easy to find the length of AE : since the point E divides the side of AA 1 in the ratio of 4 to 3 , counting from point A , and the length of the side of AA 1 is 7 , then AE = 4 . Find another length AM .
To do this, consider a right-angled triangle ABF with a right angle A , where AM is the height. By the condition AB = 2 . We can find the length of the AF side from the similarity of the right-angled triangles DD 1 F and AEF : 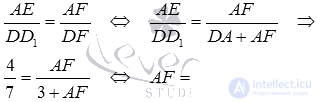
By the Pythagorean theorem from the ABF triangle we find 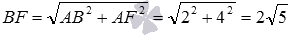 . The length of AM will be found through the area of the triangle ABF : on one side, the area of the triangle ABF is equal to
. The length of AM will be found through the area of the triangle ABF : on one side, the area of the triangle ABF is equal to 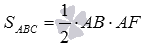 , on the other hand
, on the other hand 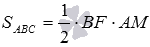 from where
from where 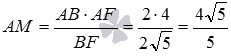 .
.
Thus, from the right triangle AEM we have 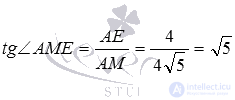 .
.
Then the required angle between the planes ABC and BED 1 is equal to 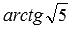 (notice, that
(notice, that 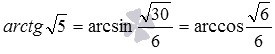 ).
).
Answer:
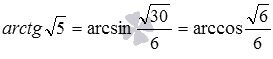
In some cases, to find the angle between two intersecting planes, it is convenient to define the rectangular coordinate system Oxyz and use the coordinate method. On it and stop.
Set the problem: find the angle between two intersecting planes  and
and  . Denote the required angle as
. Denote the required angle as 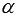 .
.
We assume that in the given rectangular coordinate system Oxyz, we know the coordinates of the normal vectors of the intersecting planes  and
and  or there is an opportunity to find them. Let be
or there is an opportunity to find them. Let be 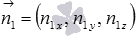 - normal plane vector
- normal plane vector  , but
, but 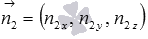 - normal plane vector
- normal plane vector  . Let us show how to find the angle between intersecting planes.
. Let us show how to find the angle between intersecting planes.  and
and  through the coordinates of the normal vectors of these planes.
through the coordinates of the normal vectors of these planes.
Denote the line on which the planes intersect  and
and  as c . Through the point M on the line c we draw the plane
as c . Through the point M on the line c we draw the plane  perpendicular to the line c . Plane
perpendicular to the line c . Plane  crosses the plane
crosses the plane  and
and  along straight lines a and b respectively, straight lines a and b intersect at point M. By definition, the angle between intersecting planes.
along straight lines a and b respectively, straight lines a and b intersect at point M. By definition, the angle between intersecting planes.  and
and  equals the angle between intersecting straight lines a and b .
equals the angle between intersecting straight lines a and b .
Set aside from point M in the plane  normal vectors
normal vectors 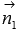 and
and 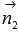 planes
planes  and
and  . With this vector
. With this vector 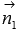 lies on a line that is perpendicular to a , and vector
lies on a line that is perpendicular to a , and vector 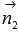 - on a straight line that is perpendicular to a straight line b . So in the plane
- on a straight line that is perpendicular to a straight line b . So in the plane 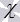 vector
vector 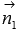 - normal vector line a ,
- normal vector line a , 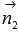 - normal vector line b .
- normal vector line b .
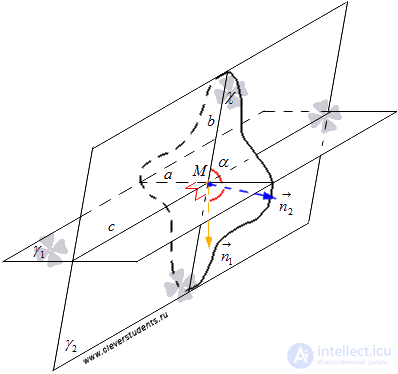
In the article, finding the angle between intersecting straight lines, we obtained a formula that allows us to calculate the cosine of the angle between intersecting straight lines along the coordinates of normal vectors. Thus, the cosine of the angle between the straight lines a and b , and, consequently, the cosine of the angle between the intersecting planes  and
and  is according to the formula
is according to the formula 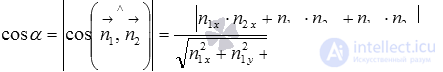 where
where 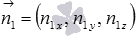 and
and 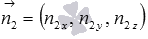 - normal vectors of planes
- normal vectors of planes  and
and  respectively. Then the angle between the intersecting planes is calculated as
respectively. Then the angle between the intersecting planes is calculated as 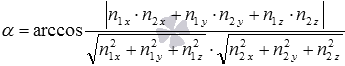 .
.
Solve the previous example using the coordinate method.
Example.
Given a rectangular parallelepiped of ABCDA 1 B 1 C 1 D 1 , in which AB = 3 , AD = 2 , AA 1 = 7 and the point E divides the side AA 1 in the ratio 4 to 3 , counting from point A. Find the angle between the ABC and BED 1 planes .
Decision.
Since the sides of a rectangular parallelepiped with one vertex are pairwise perpendicular, it is convenient to introduce the rectangular coordinate system Oxyz as follows: start to align with the vertex C , and coordinate the axes Ox , Oy and Oz to direct along the sides CD , CB and CC 1 respectively.
The angle between the ABC and BED 1 planes can be found through the coordinates of the normal vectors of these planes using the formula 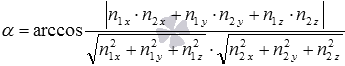 where
where 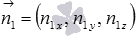 and
and 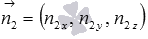 - normal vectors of planes ABC and BED 1, respectively. Determine the coordinates of normal vectors.
- normal vectors of planes ABC and BED 1, respectively. Determine the coordinates of normal vectors.
Since the ABC plane coincides with the coordinate plane Oxy , its normal vector is the coordinate vector 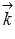 , i.e,
, i.e, 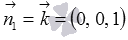 .
.
As a normal vector of the BED 1 plane, one can take the vector product of vectors 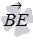 and
and 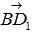 in turn, the coordinates of the vectors
in turn, the coordinates of the vectors 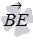 and
and 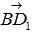 can be found through the coordinates of points B , E and D 1 (the coordinates of the vector are written in the article through the coordinates of the points of its beginning and end), and the coordinates of points B , E and D 1 in the entered coordinate system are determined from the condition of the problem.
can be found through the coordinates of points B , E and D 1 (the coordinates of the vector are written in the article through the coordinates of the points of its beginning and end), and the coordinates of points B , E and D 1 in the entered coordinate system are determined from the condition of the problem.
Obviously 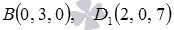 . Because
. Because 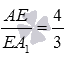 then by point coordinates
then by point coordinates 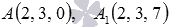 we find
we find 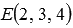 (If necessary, see the article on the division of the segment in a given relation). Then
(If necessary, see the article on the division of the segment in a given relation). Then  and
and 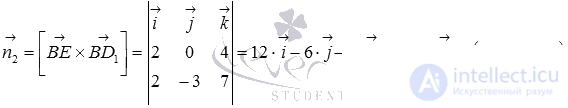
It remains to substitute the coordinates found in the formula for calculating the angle between the planes: 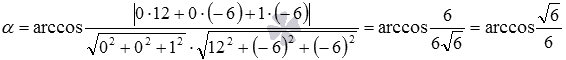
As you can see, the coordinate method gave the same result.
Answer:
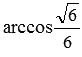
In conclusion, let us analyze the solution of the example in which we need to find the angle between the intersecting planes according to the known equations of these planes.
Example.
Find the sine of the angle, the cosine of the angle and the angle itself between the two intersecting planes defined by the equations in the rectangular coordinate system Oxyz 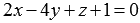 and
and 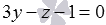 .
.
Decision.
When we studied the general equation of a straight line 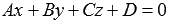 then we found out that the coefficients A , B and C are the corresponding coordinates of the normal vector of the plane. In this way,
then we found out that the coefficients A , B and C are the corresponding coordinates of the normal vector of the plane. In this way, 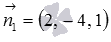 and
and 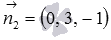 - normal vectors of planes
- normal vectors of planes 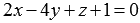 and
and 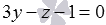 respectively.
respectively.
Substitute the coordinates of the normal vectors of the planes in the formula for calculating the angle between two intersecting planes: 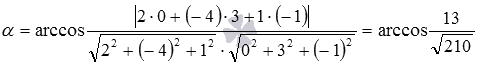
Then 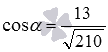 . Since the angle between two intersecting planes is not obtuse, then using the basic trigonometric identity, we find the sine of the angle:
. Since the angle between two intersecting planes is not obtuse, then using the basic trigonometric identity, we find the sine of the angle: 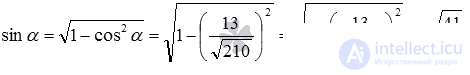 .
.
Answer:
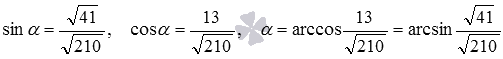
Comments
To leave a comment
Stereometry
Terms: Stereometry