Theorem Two intersecting straight lines have a common perpendicular, and with that only one. It is a common perpendicular of parallel planes passing through these straight lines.
 Evidence
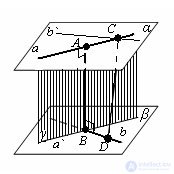
Evidence Let a and b be intersecting data. Let us draw through them the parallel planes α and β. The straight lines intersecting the straight line a and perpendicular to the plane α lie in the same plane (γ). This plane intersects the plane β along a straight line a` parallel to a. Let B be the intersection point of lines a `and b. Then the line AB, which is perpendicular to the plane α, is also perpendicular to the plane β, since β is parallel to α. The segment AB is the common perpendicular of the planes α and β, and hence the straight lines a and b.
Let us prove that this common perpendicular is unique. Suppose that the lines a and b have another common perpendicular CD. Let's draw a straight line b` through point C, parallel to b. Direct CD is perpendicular to straight line b, and therefore b`. Since it is perpendicular to line a, it is perpendicular to plane α, and therefore, parallel to line AB. It turns out that through straight lines AB and CD, as through parallel lines, it is possible to draw a plane. Our intersecting lines AC and BD will lie in this plane, and this is impossible, as was to be proved.

Comments
To leave a comment
Stereometry
Terms: Stereometry