Triangular prism volume

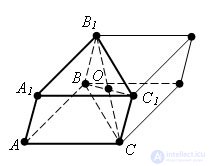
Take a triangular prism and complement it to the parallelepiped. Point O is the center of symmetry of the parallelepiped. Therefore, the completed prism is symmetric to the initial one with respect to the point O, therefore, it has a volume equal to the volume of the initial prism. Thus, the volume of the parallelepiped constructed is equal to twice the volume of this prism.

The volume of the parallelepiped is equal to the product of its base area and height. The area of ​​its base is equal to the doubled area of ​​the triangle ABC, and the height is equal to the height of the original prism. From here we conclude that the volume of the initial prism is equal to the product of its base area and height.