Theorem
If a straight line that does not belong to a plane is parallel to any straight line in this plane, then it is also parallel to the plane itself.
 Evidence
Evidence
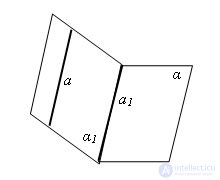
Let α be a plane, a not a line lying in it, and a1 a straight line in the plane α parallel to a. Draw the plane α1 through the lines a and a1. The planes α and α1 intersect along the straight line a1. If the line a intersected the plane α, then the intersection point would belong to the line a1. But this is impossible, since the lines a and a1 are parallel. Consequently, the line a does not intersect the plane α, and therefore is parallel to the plane α. The theorem is proved.

Comments
To leave a comment
Stereometry
Terms: Stereometry