Plane and straight

Theorem

If two points of a straight line belong to a plane, then the whole straight line belongs to this plane.



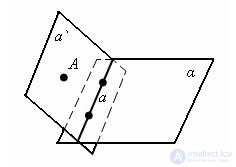
Evidence

Let a be a given straight line and α a given plane. By the planimetric axiom 1, there exists a point A that is not lying on the line a. Draw through line a and point A plane α`. If the plane α `coincides with α, then the plane α contains the line a, as stated by the theorem. If the plane α `is different from α, then these planes intersect along the straight line a`, containing two points of the straight line a