Lecture
When solving some geometric problems using the coordinate method, one has to find the coordinates of the point of intersection of the lines. Most often it is necessary to look for the coordinates of the point of intersection of two lines on a plane, but sometimes it is necessary to determine the coordinates of the point of intersection of two lines in space. In this article we will just deal with finding the coordinates of the point at which two straight lines intersect.
Let's first give a definition of the intersection point of two straight lines.
In the section, the mutual arrangement of straight lines on a plane shows that two straight lines on a plane can either coincide (they have infinitely many common points), or be parallel (and the two straight lines do not have common points), or intersect, having one common point. The variants of the mutual arrangement of two straight lines in space are larger - they can coincide (have infinitely many common points), can be parallel (that is, lie in one plane and not intersect), can be crossed (not lying in one plane), and also have one common point, that is, intersect. So, two straight lines both on the plane and in space are called intersecting if they have one common point.
From the definition of intersecting straight lines follows the definition of the intersection point of straight lines : the point at which two straight lines intersect is called the intersection point of these straight lines. In other words, the only common point of two intersecting lines is the intersection point of these lines.
For clarity, we present a graphic illustration of the point of intersection of two straight lines on a plane and in space.
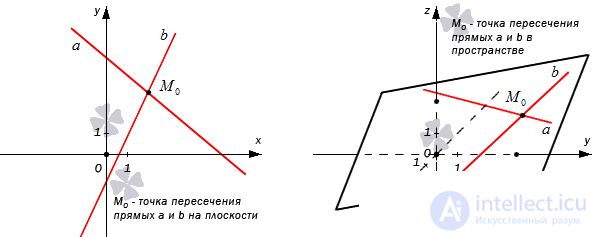
Before finding the coordinates of the intersection point of two lines on the plane by their known equations, consider the auxiliary problem.
Let a rectangular Cartesian coordinate system Oxy be fixed on a plane and two intersecting lines a and b be given . We assume that the line a corresponds to the general equation of the line 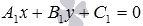 , and direct b - type
, and direct b - type 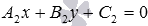 . Let be
. Let be 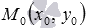 - some point of the plane, and you want to find out whether the point M 0 is the intersection point of the given straight lines.
- some point of the plane, and you want to find out whether the point M 0 is the intersection point of the given straight lines.
Solve the problem.
If M 0 is the intersection point of lines a and b , then by definition it belongs to both a and a and b , that is, its coordinates must simultaneously satisfy the equation 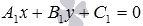 and equation
and equation 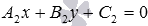 . Consequently, we need to substitute the coordinates of the point M 0 into the equations of the given straight lines and see if this results in two true equalities. If the coordinates of the point M 0 satisfy both equations
. Consequently, we need to substitute the coordinates of the point M 0 into the equations of the given straight lines and see if this results in two true equalities. If the coordinates of the point M 0 satisfy both equations 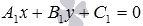 and
and 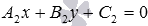 then
then 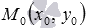 - the point of intersection of the lines a and b , otherwise M 0 is not the point of intersection of the lines.
- the point of intersection of the lines a and b , otherwise M 0 is not the point of intersection of the lines.
Example.
Is the point M 0 with coordinates (2, -3) the intersection point of straight lines 5x-2y-16 = 0 and 2x-5y-19 = 0 ?
Decision.
If M 0 is indeed the point of intersection of the given lines, then its coordinates satisfy the equations of the lines. Let us verify this by substituting the coordinates of the point M 0 into the given equations: 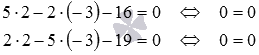
We got two true equalities, therefore, M 0 (2, -3) is the intersection point of straight lines 5x-2y-16 = 0 and 2x-5y-19 = 0 .
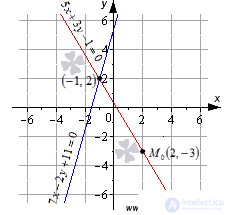
For clarity, we present a drawing in which the straight lines are shown and the coordinates of their intersection point are visible.

Answer:
yes, the point M 0 (2, -3) is the intersection point of straight lines 5x-2y-16 = 0 and 2x-5y-19 = 0 .
Example.
Do the straight lines 5x + 3y-1 = 0 and 7x-2y + 11 = 0 intersect at the point M 0 (2, -3) ?
Decision.
Substitute the coordinates of the point M 0 into the equations of straight lines, this action will be carried out checking the belonging of the point M 0 to both straight lines simultaneously: 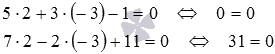
Since the second equation, when substituting the coordinates of the point M 0 into it, did not turn into a true equality, the point M 0 does not belong to the straight line 7x-2y + 11 = 0 . From this fact, we can conclude that the point M 0 is not the intersection point of the given straight lines.
It is also clearly seen in the drawing that the point M 0 is not the intersection point of straight lines 5x + 3y-1 = 0 and 7x-2y + 11 = 0 . Obviously, the given lines intersect at the point with coordinates (-1, 2) .
Answer:
M 0 (2, -3) is not the intersection of straight lines 5x + 3y-1 = 0 and 7x-2y + 11 = 0 .
Now we can proceed to the problem of finding the coordinates of the point of intersection of two straight lines by given equations of straight lines on a plane.
Let a rectangular Cartesian coordinate system Oxy be fixed on the plane and two intersecting straight lines a and b are given by the equations 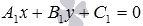 and
and 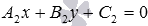 respectively. Denote the intersection point of the given straight lines as M 0 and solve the following problem: find the coordinates of the intersection point of two straight lines a and b by the known equations of these straight lines
respectively. Denote the intersection point of the given straight lines as M 0 and solve the following problem: find the coordinates of the intersection point of two straight lines a and b by the known equations of these straight lines 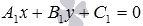 and
and 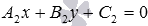 .
.
The point M 0 belongs to each of the intersecting lines a and b by definition. Then the coordinates of the intersection point of the lines a and b simultaneously satisfy the equation 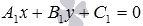 and equation
and equation 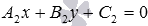 . Consequently, the coordinates of the intersection point of two straight lines a and b are the solution of the system of equations
. Consequently, the coordinates of the intersection point of two straight lines a and b are the solution of the system of equations 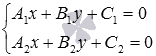 (See the article Solving Systems of Linear Algebraic Equations).
(See the article Solving Systems of Linear Algebraic Equations).
Thus, to find the coordinates of the intersection point of two lines defined on the plane by general equations, it is necessary to solve a system composed of the equations of the given lines.
Consider the solution of the example.
Example.
Find the intersection point of two straight lines defined in a rectangular coordinate system on the plane by the equations x-9y + 14 = 0 and 5x-2y-16 = 0 .
Decision.
We are given two general equations of straight lines, we will make of them a system: 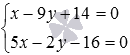 . Solutions of the resulting system of equations are easy to find if you solve its first equation for the variable x and substitute this expression in the second equation:
. Solutions of the resulting system of equations are easy to find if you solve its first equation for the variable x and substitute this expression in the second equation: 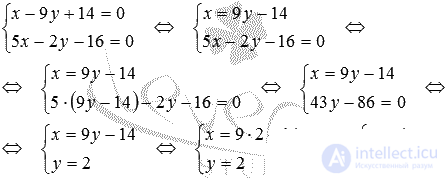
The found solution of the system of equations gives us the desired coordinates of the point of intersection of two straight lines.
Answer:
M 0 (4, 2) is the intersection point of straight lines x-9y + 14 = 0 and 5x-2y-16 = 0 .
So, finding the coordinates of the point of intersection of two lines defined by general equations on a plane reduces to solving a system of two linear equations with two unknown variables. But what if the lines on a plane are not given by general equations, but by equations of a different type (see the types of the equation of a line on a plane)? In these cases, you can first reduce the equations of the straight lines to a general form, and after that find the coordinates of the intersection point.
Example.
Determine the coordinates of the point of intersection of the lines 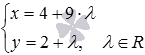 and
and 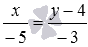 .
.
Decision.
Before finding the coordinates of the point of intersection of the given lines, we will reduce their equations to a general form. Transition from parametric equations to a line 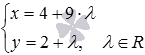 to the general equation of this line is as follows:
to the general equation of this line is as follows: 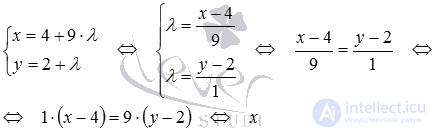
Now we carry out the necessary actions with the canonical equation of the line 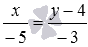 :
: 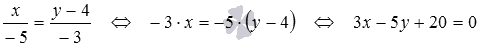
Thus, the desired coordinates of the point of intersection of the lines are the solution of the system of equations of the form  . We use the Kramer method to solve it:
. We use the Kramer method to solve it: 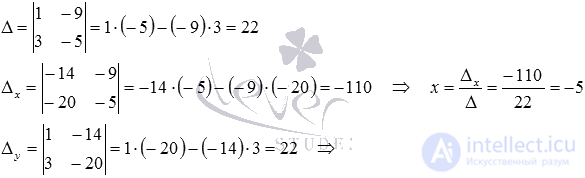
Answer:
M 0 (-5, 1)
There is another way to find the coordinates of the point of intersection of two straight lines on a plane. It is convenient to use it when one of the lines is given by parametric equations of the form 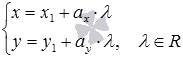 and the other is a direct equation of another type. In this case, in another equation, instead of variables x and y, you can substitute the expression
and the other is a direct equation of another type. In this case, in another equation, instead of variables x and y, you can substitute the expression 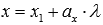 and
and  where you can get the value
where you can get the value 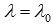 which corresponds to the intersection point of the given straight lines. The point of intersection of the lines has coordinates
which corresponds to the intersection point of the given straight lines. The point of intersection of the lines has coordinates 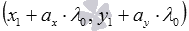 .
.
Find the coordinates of the point of intersection of lines from the previous example in this way.
Example.
Determine the coordinates of the point of intersection of the lines 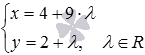 and
and 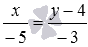 .
.
Decision.
Substitute in the equation of the line 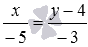 expressions
expressions 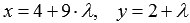 :
: 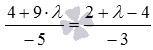
Having solved the resulting equation, we get 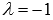 . This value corresponds to the common point of straight lines.
. This value corresponds to the common point of straight lines. 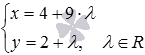 and
and 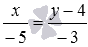 . We calculate the coordinates of the intersection point, substituting
. We calculate the coordinates of the intersection point, substituting 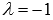 in parametric equations of a straight line:
in parametric equations of a straight line: 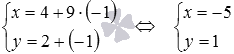 .
.
Answer:
M 0 (-5, 1) .
To complete the picture should discuss one more thing.
Before finding the coordinates of the intersection point of two straight lines on the plane, it is useful to make sure that the given straight lines really intersect. If it turns out that the original lines coincide or are parallel, then finding the coordinates of the intersection point of such lines is out of the question.
You can, of course, do without such a test, and immediately form a system of equations of the form 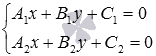 and solve it. If the system of equations has a unique solution, then it gives the coordinates of the point at which the original lines intersect. If the system of equations does not have a solution, then we can conclude that the original straight lines are parallel (since there is no such pair of real numbers x and y that would satisfy both equations of the given straight lines). From the presence of an infinite set of solutions to the system of equations, it follows that the original lines have infinitely many common points, that is, they coincide.
and solve it. If the system of equations has a unique solution, then it gives the coordinates of the point at which the original lines intersect. If the system of equations does not have a solution, then we can conclude that the original straight lines are parallel (since there is no such pair of real numbers x and y that would satisfy both equations of the given straight lines). From the presence of an infinite set of solutions to the system of equations, it follows that the original lines have infinitely many common points, that is, they coincide.
Consider examples suitable for these situations.
Example.
Find out if the lines intersect. 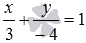 and
and 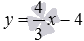 , and if intersect, then find the coordinates of the intersection point.
, and if intersect, then find the coordinates of the intersection point.
Decision.
The equations of the lines correspond to the equations 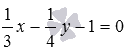 and
and 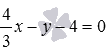 . Solve a system composed of these equations.
. Solve a system composed of these equations. 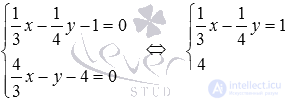 .
.
It is obvious that the equations of the system are linearly expressed through each other (the second equation of the system is obtained from the first by multiplying both its parts by 4 ), therefore, the system of equations has an infinite number of solutions. So the equations 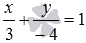 and
and 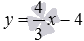 define the same straight line, and we cannot talk about finding the coordinates of the intersection point of these straight lines.
define the same straight line, and we cannot talk about finding the coordinates of the intersection point of these straight lines.
Answer:
the equations 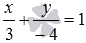 and
and 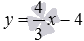 define in the rectangular coordinate system Oxy the same straight line, so we can not talk about finding the coordinates of the intersection point.
define in the rectangular coordinate system Oxy the same straight line, so we can not talk about finding the coordinates of the intersection point.
Example.
Find the coordinates of the point of intersection of lines 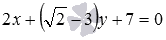 and
and 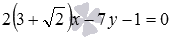 , if possible.
, if possible.
Decision.
The condition of the problem assumes that the lines can be non-intersecting. Build a system of these equations. Let us apply the Gauss method to solve it, since it allows to establish the compatibility or incompatibility of the system of equations, and if it is compatible, find a solution: 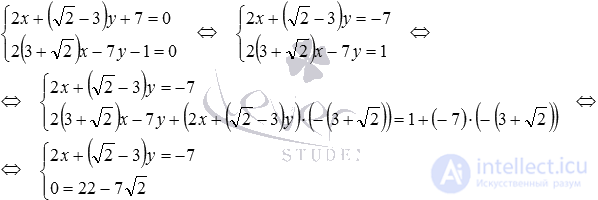
The last equation of the system after the direct course of the Gauss method turned into an incorrect equality, therefore, the system of equations has no solutions. From this we can conclude that the original straight lines are parallel, and we cannot talk about finding the coordinates of the intersection point of these straight lines.
The second solution.
Let's find out if the given lines intersect.
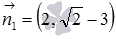 - normal straight line vector
- normal straight line vector 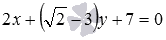 and vector
and vector 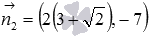 is a normal straight line vector
is a normal straight line vector 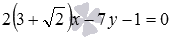 . Check the fulfillment of the condition of collinearity of vectors
. Check the fulfillment of the condition of collinearity of vectors 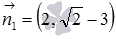 and
and 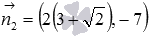 : equality
: equality 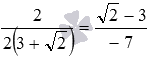 true since
true since 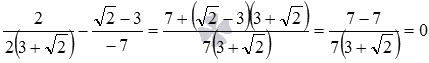 therefore, the normal vectors of the given straight lines are collinear. Then, these lines are parallel or coincide. Thus, we cannot find the coordinates of the point of intersection of the original lines.
therefore, the normal vectors of the given straight lines are collinear. Then, these lines are parallel or coincide. Thus, we cannot find the coordinates of the point of intersection of the original lines.
Answer:
the coordinates of the point of intersection of the given lines cannot be found, since these lines are parallel.
Example.
Find the coordinates of the intersection point of straight lines 2x-1 = 0 and 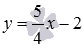 if they intersect.
if they intersect.
Decision.
Let's make a system of equations, which are the general equations of the given straight lines: 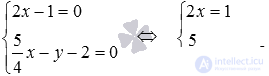 . The determinant of the main matrix of this system of equations is non-zero.
. The determinant of the main matrix of this system of equations is non-zero. 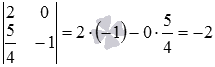 therefore, the system of equations has a unique solution, which indicates the intersection of the given straight lines.
therefore, the system of equations has a unique solution, which indicates the intersection of the given straight lines.
To find the coordinates of the point of intersection of the lines, we need to solve the system: 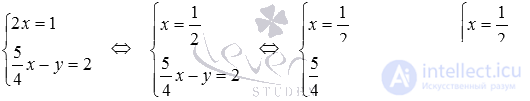
The resulting solution gives us the coordinates of the point of intersection of the lines, that is, 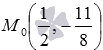 - the point of intersection of straight lines 2x-1 = 0 and
- the point of intersection of straight lines 2x-1 = 0 and 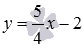 .
.
Answer:
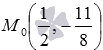
The coordinates of the intersection point of two straight lines in three-dimensional space are found similarly.
Let the intersecting straight lines a and b are given in a rectangular coordinate system Oxyz by the equations of two intersecting planes, that is, the straight line a is defined by a system of the form 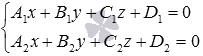 , and direct b -
, and direct b - 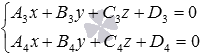 . Let M 0 be the intersection point of lines a and b . Then the point M 0, by definition, belongs to both the straight line a and the straight line b , therefore, its coordinates satisfy the equations of both straight lines. Thus, the coordinates of the point of intersection of the lines a and b represent a solution of a system of linear equations of the form
. Let M 0 be the intersection point of lines a and b . Then the point M 0, by definition, belongs to both the straight line a and the straight line b , therefore, its coordinates satisfy the equations of both straight lines. Thus, the coordinates of the point of intersection of the lines a and b represent a solution of a system of linear equations of the form 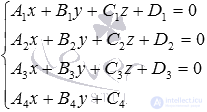 . Here we find useful information from the section on the resolution of systems of linear equations in which the number of equations does not coincide with the number of unknown variables.
. Here we find useful information from the section on the resolution of systems of linear equations in which the number of equations does not coincide with the number of unknown variables.
Consider solving examples.
Example.
Find the coordinates of the intersection point of two lines defined in the space of equations 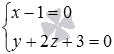 and
and 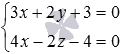 .
.
Decision.
Let's make a system of equations from the equations of the given straight lines: 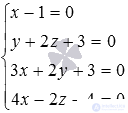 . The solution of this system will give us the desired coordinates of the point of intersection of straight lines in space. Find the solution of the written system of equations.
. The solution of this system will give us the desired coordinates of the point of intersection of straight lines in space. Find the solution of the written system of equations.
The main matrix of the system is 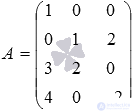 and extended -
and extended - 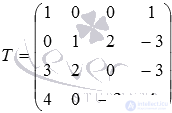 .
.
We define the rank of the matrix A and the rank of the matrix T. We use the method of bordering minors, but we will not describe in detail the calculation of determinants (if necessary, refer to the article calculating the determinant of a matrix): 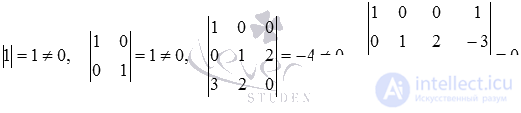
Thus, the rank of the main matrix is equal to the rank of the expanded matrix and is equal to three.
Therefore, the system of equations 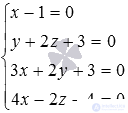 has the only solution.
has the only solution.
Base minor will take the determinant 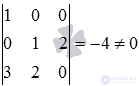 therefore, the last equation should be excluded from the system of equations, since it does not participate in the formation of the basis minor. So,
therefore, the last equation should be excluded from the system of equations, since it does not participate in the formation of the basis minor. So, 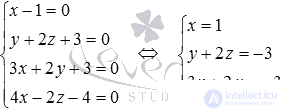
The solution of the resulting system is easily located: 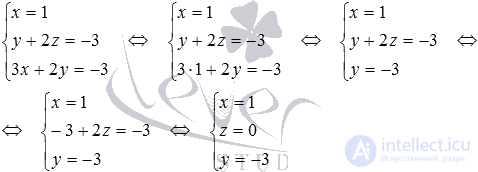
Thus, the point of intersection of the lines 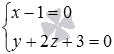 and
and 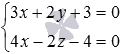 has coordinates (1, -3, 0) .
has coordinates (1, -3, 0) .
Answer:
(1, -3, 0) .
It should be noted that the system of equations 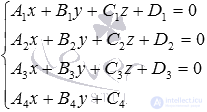 has a unique solution if and only if the lines a and b intersect. If the lines a and b are parallel or intersecting, then the latter system of equations has no solution, since in this case the lines have no common points. If the lines a and b coincide, then they have an infinite set of common points, therefore, this system of equations has an infinite set of solutions. However, in these cases we cannot talk about finding the coordinates of the point of intersection of the lines, since the lines are not intersecting.
has a unique solution if and only if the lines a and b intersect. If the lines a and b are parallel or intersecting, then the latter system of equations has no solution, since in this case the lines have no common points. If the lines a and b coincide, then they have an infinite set of common points, therefore, this system of equations has an infinite set of solutions. However, in these cases we cannot talk about finding the coordinates of the point of intersection of the lines, since the lines are not intersecting.
Thus, if we do not know in advance whether the given straight lines a and b intersect or not, then it is reasonable to make a system of equations of the form 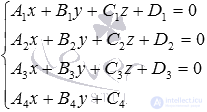 and solve it by the Gauss method. If we obtain a unique solution, then it will correspond to the coordinates of the intersection point of lines a and b . If the system proves to be inconsistent, then the lines a and b do not intersect. If the system has an infinite set of solutions, then the lines a and b coincide.
and solve it by the Gauss method. If we obtain a unique solution, then it will correspond to the coordinates of the intersection point of lines a and b . If the system proves to be inconsistent, then the lines a and b do not intersect. If the system has an infinite set of solutions, then the lines a and b coincide.
You can do without the use of the Gauss method. Alternatively, one can calculate the ranks of the basic and extended matrices of this system, and based on the data obtained and the Kronecker-Capelli theorem, one can conclude either about the existence of a single solution, or about the existence of a set of solutions, or about the absence of solutions. It's a matter of taste.
Example.
If straight 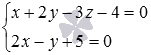 and
and 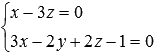 intersect, then determine the coordinates of the intersection point.
intersect, then determine the coordinates of the intersection point.
Decision.
Let's make a system of the given equations: 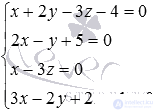 . We solve it by the Gauss method in the matrix form:
. We solve it by the Gauss method in the matrix form: 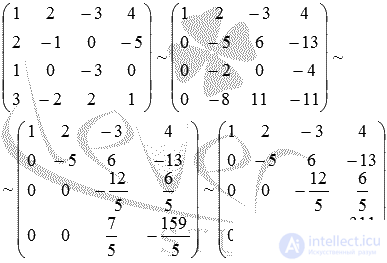
It became clear that the system of equations has no solutions, therefore, the given straight lines do not intersect, and there can be no question of finding the coordinates of the intersection point of these straight lines.
Answer:
we cannot find the coordinates of the intersection point of given straight lines, since these straight lines do not intersect.
When intersecting lines are given by canonical equations of a line in space or by parametric equations of a line in space, you should first obtain their equations in the form of two intersecting planes, and then find the coordinates of the intersection point.
Example.
Two intersecting lines are given in the Oxyz rectangular coordinate system by equations 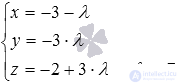 and
and 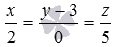 . Find the coordinates of the intersection point of these lines.
. Find the coordinates of the intersection point of these lines.
Decision.
Let's set the initial straight lines by the equations of two intersecting planes: 
To find the coordinates of the point of intersection of the straight lines, it remains to solve the system of equations 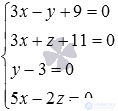 . The rank of the main matrix of this system is equal to the rank of the expanded matrix and is equal to three (we recommend checking this fact). As a basic minor take
. The rank of the main matrix of this system is equal to the rank of the expanded matrix and is equal to three (we recommend checking this fact). As a basic minor take 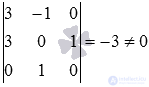 therefore, the last equation can be eliminated from the system.
therefore, the last equation can be eliminated from the system. 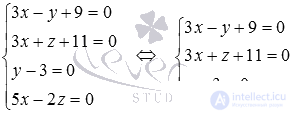 . Solving the resulting system by any method (for example, the Kramer method) we get the solution
. Solving the resulting system by any method (for example, the Kramer method) we get the solution 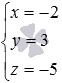 . Thus, the point of intersection of the lines
. Thus, the point of intersection of the lines 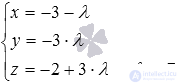 and
and 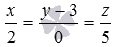 has coordinates (-2, 3, -5) .
has coordinates (-2, 3, -5) .
Answer:
(-2, 3, -5) .
Comments
To leave a comment
Stereometry
Terms: Stereometry