Lecture
In this article we will answer the question: “How to find the coordinates of the point of intersection of a straight line and a plane, if the equations defining the straight line and the plane are given”? We start with the concept of the intersection point of a line and a plane. Next, we show two ways to find the coordinates of the point of intersection of a line and a plane. To consolidate the material consider the detailed solutions of examples.
The heading of the article includes the words "point", "straight line" and "plane". Therefore, to understand the topic, it is necessary to have a clear idea of a point, a straight line and a plane in space. You can refresh these concepts in your memory by referring to articles straight in space and a plane in space.
There are three options for the relative position of the line and the plane in space:
We are interested in the third case. Recall what the phrase means: "straight line and plane intersect." A straight line and a plane are said to intersect if they have only one common point. This common point of the intersecting straight line and the plane is called the intersection point of the straight line and the plane .
We give a graphic illustration.

We introduce in a three-dimensional space a rectangular coordinate system Oxyz . Now, each straight line corresponds to a straight line equation of a certain type (the article describes the types of equations of a straight line in space), each plane corresponds to the plane equation (you can read the article kinds of plane equation), and each point corresponds to an ordered triple of numbers — the coordinates of the point. The further presentation implies knowledge of all types of equations of a straight line in space and all types of equations of a plane, as well as the ability to move from one type of equations to another type. But do not worry, the text we will provide links to the necessary theory.
Let us first analyze in detail the problem, the solution of which we can obtain based on the definition of the point of intersection of the line and the plane. This task will prepare us for finding the coordinates of the point of intersection of the line and the plane.
Example.
Is the point M 0 with coordinates 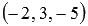 intersection point
intersection point 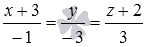 and planes
and planes  .
.
Decision.
We know that if a point belongs to some straight line, then the coordinates of the point satisfy the equations of the straight line. Similarly, if a point lies in a certain plane, then the coordinates of the point satisfy the equation of this plane. By definition, the point of intersection of a straight line and a plane is a common point of a straight line and a plane; then the coordinates of the intersection point satisfy both the equations of the straight line and the equation of the plane.
Thus, to solve the problem, we should substitute the coordinates of the point M 0 into the given equations of the line and into the equation of the plane. If all the equations turn to true equalities, then the point M 0 is the intersection point of the given line and the plane, otherwise the point M 0 is not the point of intersection of the line and the plane.
Substitute the coordinates of the point  :
: 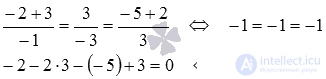
All equations turned into true equalities, therefore, the point M 0 belongs simultaneously and direct 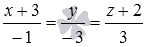 and planes
and planes  that is, M 0 is the intersection point of the indicated straight line and plane.
that is, M 0 is the intersection point of the indicated straight line and plane.
Answer:
yes point  - this is the point of intersection of the line
- this is the point of intersection of the line 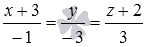 and planes
and planes  .
.
So, the coordinates of the point of intersection of the line and the plane satisfy both the equations of the line and the equation of the plane. We will use this fact when finding the coordinates of the point of intersection of the line and the plane.
The first way to find the coordinates of the point of intersection of a line and a plane.
Let the straight line a and the plane be given in the rectangular coordinate system Oxyz 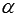 and it is known that the straight line a and the plane
and it is known that the straight line a and the plane 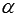 intersect at point M 0 .
intersect at point M 0 .
Find the coordinates of the point M 0 for the case when the plane 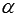 given by the general equation of the plane of the form
given by the general equation of the plane of the form 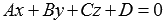 and the line a is the intersection of two planes.
and the line a is the intersection of two planes. 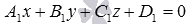 and
and 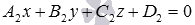 (this method of defining a straight line in space is devoted to an article of the equation of a straight line - the equation of two intersecting planes).
(this method of defining a straight line in space is devoted to an article of the equation of a straight line - the equation of two intersecting planes).
The desired coordinates of the point of intersection of the line a and the plane 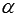 , as we have said, satisfy both the equations of the line a and the equation of the plane
, as we have said, satisfy both the equations of the line a and the equation of the plane 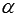 therefore, they can be found as a solution of a system of linear equations of the form
therefore, they can be found as a solution of a system of linear equations of the form 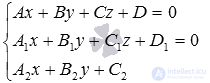 . This is indeed the case, since the solution of a system of linear equations turns every equation of the system into an identity.
. This is indeed the case, since the solution of a system of linear equations turns every equation of the system into an identity.
Note that with this formulation of the problem, we actually find the coordinates of the intersection point of the three planes given by the equations 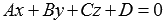 ,
, 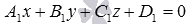 and
and 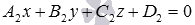 .
.
Let's solve an example for fixing the material.
Example.
The line defined by the equations of two intersecting planes as 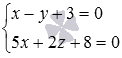 crosses the plane
crosses the plane 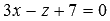 . Find the coordinates of the point of intersection of the line and the plane.
. Find the coordinates of the point of intersection of the line and the plane.
Decision.
We obtain the required coordinates of the point of intersection of the line and the plane by solving a system of equations of the form 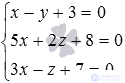 . In this case, we will rely on the article’s information on solving systems of linear equations.
. In this case, we will rely on the article’s information on solving systems of linear equations.
To begin with, we will rewrite the system of equations in the form 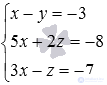 and calculate the determinant of the main matrix of the system (if necessary, refer to the article for calculating the determinant of the matrix):
and calculate the determinant of the main matrix of the system (if necessary, refer to the article for calculating the determinant of the matrix): 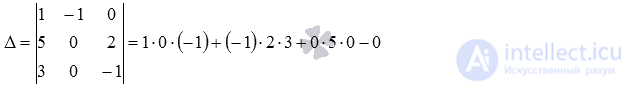
The determinant of the main matrix of the system is nonzero, so the system of equations has a unique solution. To find it, you can use any method. We use the Cramer method: 
So we got the coordinates of the point of intersection of the line and the plane (-2, 1, 1) .
Answer:
(-2, 1, 1) .
It should be noted that the system of equations 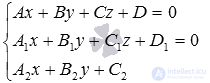 has the only solution if the line a , defined by the equations
has the only solution if the line a , defined by the equations 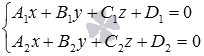 and plane
and plane 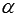 given by equation
given by equation 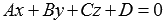 intersect. If the line a lies in the plane
intersect. If the line a lies in the plane 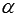 , the system has an infinite number of solutions. If the line a is parallel to the plane
, the system has an infinite number of solutions. If the line a is parallel to the plane 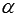 , then the system of equations has no solution.
, then the system of equations has no solution.
Example.
Find the point of intersection of the line 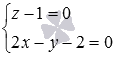 and planes
and planes 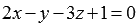 , if possible.
, if possible.
Decision.
The clause "if possible" means that the straight line and the plane may not intersect.
Build a system of given equations 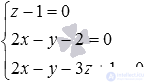 . If this system of equations has a unique solution, then it will give us the desired coordinates of the point of intersection of the line and the plane. If this system has no solutions or infinitely many solutions, then finding the coordinates of the intersection point is out of the question, since the straight line is either parallel to the plane or lies in this plane.
. If this system of equations has a unique solution, then it will give us the desired coordinates of the point of intersection of the line and the plane. If this system has no solutions or infinitely many solutions, then finding the coordinates of the intersection point is out of the question, since the straight line is either parallel to the plane or lies in this plane.
The main matrix of the system is  and the extended matrix is
and the extended matrix is  . Determine the rank of the matrix A and the rank of the matrix T by the method of bordering minors:
. Determine the rank of the matrix A and the rank of the matrix T by the method of bordering minors:  . That is, the rank of the main matrix is equal to the rank of the expanded matrix of the system and is equal to two. Consequently, based on the Kronecker-Capelli theorem, it can be argued that the system of equations has an infinite number of solutions.
. That is, the rank of the main matrix is equal to the rank of the expanded matrix of the system and is equal to two. Consequently, based on the Kronecker-Capelli theorem, it can be argued that the system of equations has an infinite number of solutions.
So direct 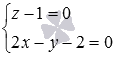 lies in the plane
lies in the plane 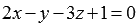 and we cannot talk about finding the coordinates of the point of intersection of the line and the plane.
and we cannot talk about finding the coordinates of the point of intersection of the line and the plane.
Answer:
It is impossible to find the coordinates of the intersection point of a line and a plane.
Example.
If straight 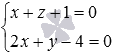 intersects with the plane
intersects with the plane 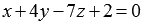 then find the coordinates of their intersection point.
then find the coordinates of their intersection point.
Decision.
Build a system of given equations 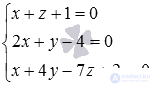 . To find its solution, we use the Gauss method. The Gauss method will allow us not only to determine whether the written system of equations has one solution, an infinite set of solutions or does not have a single solution, but also to find solutions if they exist.
. To find its solution, we use the Gauss method. The Gauss method will allow us not only to determine whether the written system of equations has one solution, an infinite set of solutions or does not have a single solution, but also to find solutions if they exist. 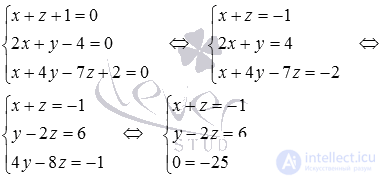
The last equation of the system after the direct course of the Gauss method became an incorrect equality, therefore, the system of equations has no solutions. Hence we conclude that the straight line 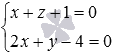 and the plane
and the plane 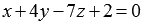 do not have common points. Thus, we cannot talk about finding the coordinates of their intersection point.
do not have common points. Thus, we cannot talk about finding the coordinates of their intersection point.
Answer:
the line is parallel to the plane and they do not have an intersection point.
Note that if the straight line a corresponds to the parametric equations of a straight line in space or the canonical equations of a straight line in space, then we can get the equations of two intersecting planes defining the straight line a , and then find the coordinates of the intersection point of the straight line a and the plane 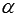 disassembled way. However, it is easier to use another method, to the description of which we turn.
disassembled way. However, it is easier to use another method, to the description of which we turn.
The second way to find the coordinates of the point of intersection of a line and a plane.
Suppose that in the rectangular coordinate system Oxyz, the line a intersects the plane 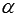 at point M 0 . Find the coordinates of the point M 0 for the case when the plane
at point M 0 . Find the coordinates of the point M 0 for the case when the plane 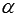 given by the general equation of the plane of the form
given by the general equation of the plane of the form 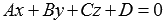 , and the straight line and is determined by parametric equations of the form
, and the straight line and is determined by parametric equations of the form 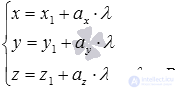 .
.
If in equation 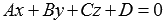 substitute expressions
substitute expressions 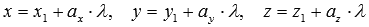 , we come to the equation with the unknown
, we come to the equation with the unknown 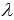 . Solving this equation for
. Solving this equation for 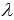 we will get the value
we will get the value 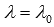 corresponding to the coordinates of the point of intersection of the line a and the plane
corresponding to the coordinates of the point of intersection of the line a and the plane 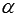 . The coordinates of the point of intersection of the line and the plane are calculated as
. The coordinates of the point of intersection of the line and the plane are calculated as 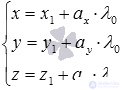 .
.
Let us analyze this method of finding the coordinates of the point of intersection of a straight line and a plane using an example.
Example.
Find the coordinates of the point of intersection of the line 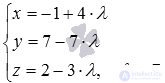 and planes
and planes 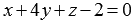 .
.
Decision.
Substitute in the equation of the plane of expression 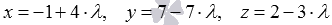 :
: 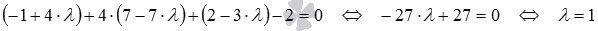
Find the coordinates of the point of intersection of the line and the plane by parametric equations with 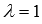 :
: 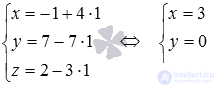
Answer:
(3, 0, -1) .
Please note: if direct 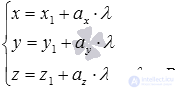 lies in the plane
lies in the plane 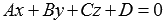 then substituting in the equation
then substituting in the equation 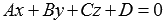 expressions
expressions 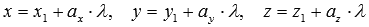 we will get identity
we will get identity 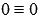 and if the specified straight line is parallel to the plane, then we get the wrong equality.
and if the specified straight line is parallel to the plane, then we get the wrong equality.
In conclusion, let us say the case when the line a is given by canonical equations of the form 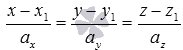 . In this case, to find the coordinates of the point of intersection of the line a with the plane
. In this case, to find the coordinates of the point of intersection of the line a with the plane 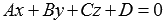 , it is necessary to pass from the canonical equations of a straight line to the parametric equations of this straight line (
, it is necessary to pass from the canonical equations of a straight line to the parametric equations of this straight line ( 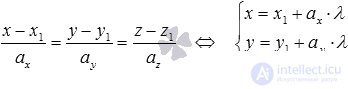 ) and use the disassembled method.
) and use the disassembled method.
Comments
To leave a comment
Stereometry
Terms: Stereometry