Plane and point

Theorem

It is possible to draw a plane through a straight line and a point not lying on it, and only one.



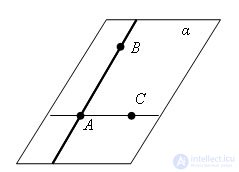Evidence

Let AB be a given line and C not a point lying on it. Draw through points A and C a straight line. The straight lines AB and AC are different, since the point C does not lie on the straight line AB. Draw the lines α through the lines AB and AC. It passes through line AB and point C.
We prove that the plane α passing through the straight line AB and the point C is unique.
Suppose there is another plane α.`, passing through line AB and point C. According to the axiom that if two different planes have a common point, then they intersect in a line passing through this point, the plane α and α` intersect along straight. This line must contain points A, B, C. But they do not lie on one line. That contradicts the assumption. The theorem is proved.