In order to find the volume of a rectangular parallelepiped with linear dimensions a, b, c, we prove that the volumes of two rectangular parallelepipeds with equal bases are referred to as their heights.
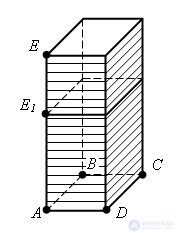
Let P and P1 be two rectangular parallelepipeds with a common base ABCD and heights AE and AE1. We assume for definiteness that AE1 <AE. Let V and V1 be the volumes of parallelepipeds. Divide the edge AE of the parallelepiped P into a large number n equal parts. Each of them is equal to AE / n. Let m be the number of division points that lie on the edge AE1. Then
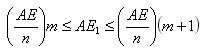
From here

Draw through the dividing points of the plane parallel to the base. They will divide the parallelepiped P into n equal parallelepipeds. Each of them has a volume V / n. The parallelepiped P1 contains the first m parallelepipeds, counting from below, and is contained in m + 1 parallelepipeds. therefore
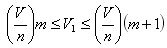
From here
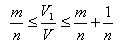
Since V1 / V and AE1 / AE are between m / n and m / n + 1 / n, they differ by no more than 1 / n. And since n can be taken arbitrarily large, it can only be at
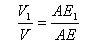
Q.E.D.
We now take a cube, which is a unit of measurement for volume, and three rectangular parallelepipeds with dimensions: a, 1, 1; a, b, 1; a, b, c. We denote their volumes V1, V2 and V, respectively. According to proven
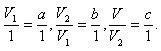
Multiplying these equalities term by term, we get: V = abc

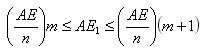

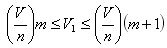
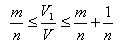
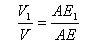
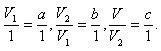
Comments
To leave a comment
Stereometry
Terms: Stereometry