Similarity of spatial figures

The transformation of a figure F is called a similarity transformation , if in this transformation the distances between points change the same number of times, i.e. for any two points X and Y figures F and points X`, Y` figures F`, into which they pass X`Y` = k * XY.
Two figures are called similar if they are translated one into another by a similarity transformation.

The similarity transformation in space is defined in the same way as on a plane . Namely: the transformation of a figure F is called a similarity transformation, if during this transformation the distances between points change the same number of times, i.e. for any two points X and Y of figure F and points X ', Y of figure F', which they move, X'Y '= k . Xy.

Just as on a plane, the similarity transformation in space translates straight lines into straight lines, half-lines into semi-straight lines, segments into segments and preserves the angles between the half-lines. By the same reasoning as in § 157, it is proved that the similarity transformation translates planes in a plane. As on the plane, two figures are called similar if they are translated one into another by a similarity transformation.

The simplest transformation of similarity in space is homothety. As well as on the plane, the homothety about the center O with the homothety coefficient k is a transformation that takes an arbitrary point X to a point X 'of the OX ray, such that OX' = k . OX.

The transformation of a homothety in space takes any plane that does not pass through the center of the homothety into a parallel plane (or into itself with k = 1).

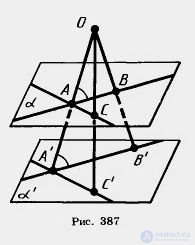
Indeed, let O be the center of homothety and 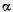- any plane not passing through the point O (fig. 387). Take any line AB in the plane 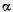. The homothety transformation translates point A to point A 'on the OA ray, and point B to point B' on the OB ray, and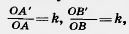
k is the homothety coefficient. This implies the similarity of triangles AOB and A'OV '. From the similarity of triangles it follows that the respective angles OAB and OA'B ', and, therefore, the parallelism of straight lines AB and A'B', are equal.

Now take another straight speaker in the plane 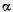. It will go to parallel straight line A'C 'with homothety. At the homothety under consideration, the plane 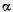go to the plane 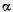',' passing through the straight A'B ', A'S. Since A'V'llAB and A'C'll AS, then by Theorem 16.4 plane 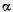and 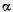'parallel, as required .