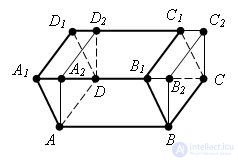
Let there be a parallelepiped ABCDA1B1C1D1. Draw a plane perpendicular to the base ABCD through the edge BC and add the inclined parallelepiped with a triangular prism BB1B2CC1C2. We now cut off the triangular prism from the resulting body with a plane passing through the edge AD and perpendicular to the base ABCD. Then we get the parallelepiped again. This parallelepiped has a volume equal to the volume of the original parallelepiped.
The completed prism and the cut-off are combined by parallel transfer to the segment AB, therefore, they have the same volumes. In the described transformation of the parallelepiped, the area of its base and height are preserved. The planes of the two side faces are also preserved, while the other two become perpendicular to the base.
Applying such a transformation once again to inclined faces, we obtain a parallelepiped, in which all the lateral faces are perpendicular to the base, i.e. straight parallelepiped.
Comments