Theorem The area of the orthogonal projection of the polygon on the plane is equal to the product of its area and the cosine of the angle between the plane of the polygon and the projection plane.
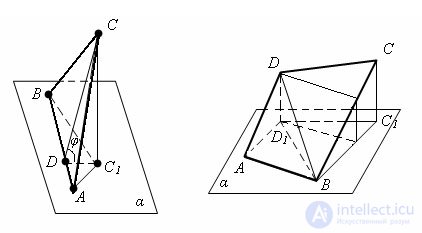
Evidence.
Let there be a triangle ABC and its projection ABC1 on the plane α. Conduct the height of the CD triangle ABC. By the three perpendiculars theorem, the segment C1D is the height of the triangle ABC1. The angle CDC1 is equal to the angle φ between the plane of the triangle ABC and the projection plane α.
Therefore, the theorem is true for a triangle.
Suppose now there is a polygon ABCD. Divide it into triangles. Each triangle that has no side parallel to the projection plane is divided into two triangles with a common side parallel to the projection plane. We get that for each triangle Δ and its projection Δ` in the plane α the equality is true
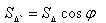
Add up all these equalities term by term. Will get
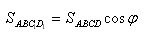
The theorem is proved.

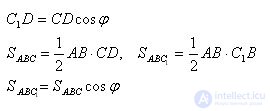
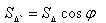
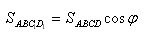
Comments
To leave a comment
Stereometry
Terms: Stereometry