There is an arbitrary pyramid. Divide its base into triangles Δ1, Δ 2, ..., Δn. Pyramids, whose bases are these triangles, and the vertices are the vertex of a given pyramid, make up this pyramid. The volume of this pyramid is equal to the sum of the volumes of the pyramids comprising it. Since they all have the same height H as this pyramid, its volume is equal to:
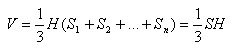
The volume of any pyramid is equal to one third of the product of its base area to a height.
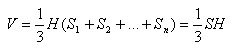
Comments
To leave a comment
Stereometry
Terms: Stereometry