Two planes are called
parallel if they do not intersect.
Theorem
If two intersecting straight lines of one plane are respectively parallel to two straight lines of another plane, then these planes are parallel.
 Evidence
Evidence
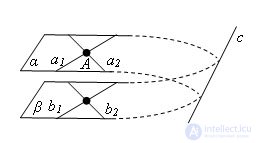
Let α and β be the given planes, a1 and a2 are straight lines in the α plane, intersecting at point A, b1 and b2 are, respectively, straight lines parallel to them in the β plane.
Suppose that the planes α and β are not parallel, and therefore intersect along some straight line c. According to the theorem on the parallelism of a straight line and a plane, straight lines a1 and a2, as parallel straight lines b1 and b2, are parallel to the plane β, and therefore they do not intersect the straight line c lying in this plane. Thus, in the plane α through lines A pass the lines a1 and a2, parallel to the line c. This is impossible according to the parallel axiom. That contradicts the assumption. The theorem is proved.

Comments
To leave a comment
Stereometry
Terms: Stereometry