Sign of parallel lines in space

Theorem

Two straight lines parallel to the third straight line are parallel.



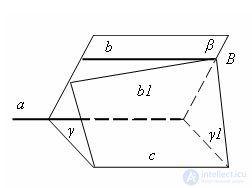
Evidence

Let straight lines b and c be parallel to a line a. It is necessary to prove that the lines b and c are parallel.
The case when the lines a, b, c lie in the same plane is considered in the section parallel straight lines.
Let the lines do not lie in the same plane and β is the plane in which the lines a and b lie, and γ is the plane in which lines a and c lie. The planes β and γ are different. We mark some point B on the line b and draw the plane γ1 through the line c and point B. It will cross the plane β along the line b1.
The straight line b1 does not intersect the plane γ. Indeed, the intersection point must belong to the line a, since the straight line b1 lies in the plane β. On the other hand, it must lie on the line c, since the straight line b1 lies in the plane γ1. But the lines a and c as parallel do not intersect.
Since the straight line b1 lies in the plane β and does not intersect the straight line a, it is parallel to a, which means it coincides with b in the parallel axiom. Hence, the straight line b, coinciding with the straight line b1, lies in the same plane with the straight line c (in the plane γ1) and does not intersect it and the straight lines b and c are parallel. The theorem is proved.