Motion in space is called a transform, which maintains the distance between points.
Movement in space has the same properties as in the plane and another new one: movement translates planes in the plane.
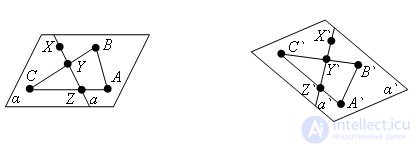 Evidence
Evidence Let α be an arbitrary plane. Take on it three arbitrary points A, B and C, which are not lying on one straight line. When moving, they will move to A`, B`, C`, also not lying on one straight line. We will pass through them the flatness α`.
We prove that with such a motion, the plane α passes into the plane α`.
Let X be an arbitrary point of the plane α. Let us draw through some straight line a in the plane α, intersecting triangle ABC at two points Y and Z, straight line a will pass to points Y` and Z` belonging to triangle A`B`C`, which means that plane α`.
Hence, the straight line a` lies in the plane α`. The point X, when moving, goes to the point X` of the line a`, and hence the plane α`, which was to be proved.
In space, two figures are called
equal if they are combined by movement.

Comments
To leave a comment
Stereometry
Terms: Stereometry