Property of lines perpendicular to the plane

Theorem

Two straight lines, perpendicular to the same plane, are parallel.



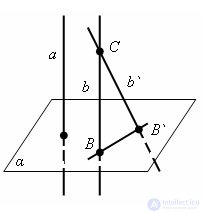
Evidence

Let a and b be two straight lines perpendicular to the plane α.
Suppose that the lines a and b are not parallel.
Choose a point C on the line b that is not in the plane α. Draw a line b` through point C parallel to a. The straight line b` is perpendicular to the plane α. Let B and B` be the intersection points of lines b and b` with the plane α. Then the straight line BB` is perpendicular to the intersecting straight lines b and b`. And this is impossible and contrary to the assumption. The theorem is proved.