Lecture
|
We begin this article with the definition of the angle between a straight line and a plane. After this, we will show how the angle between the straight line and the plane is found by the method of coordinates, analyze in detail the solutions of typical examples and problems.
Before talking about the definition of the angle between a straight line and a plane, we recommend refreshing the concept of a straight line in space and the concept of a plane.
To determine the angle between a straight line and a plane, we need several auxiliary definitions. We give these definitions.
Definition
A line and a plane intersect if they have one single common point, which is called the point of intersection of the line and the plane .

In this case, the straight line that intersects the plane can be perpendicular to this plane.
Definition
A straight line is perpendicular to a plane if it is perpendicular to any straight line lying in that plane.
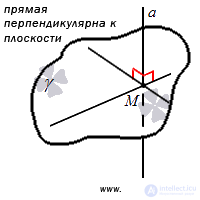
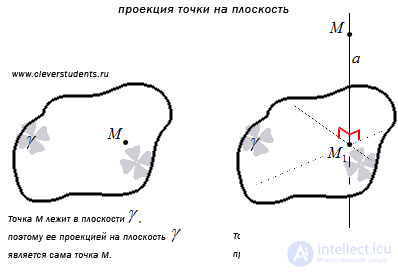
Definition
The projection of the point M on the plane  is called either the point M itself, if M lies in the plane
is called either the point M itself, if M lies in the plane  , or the intersection point of the plane
, or the intersection point of the plane  and straight, perpendicular to the plane
and straight, perpendicular to the plane  and passing through the point M , if the point M does not lie in the plane
and passing through the point M , if the point M does not lie in the plane  .
.
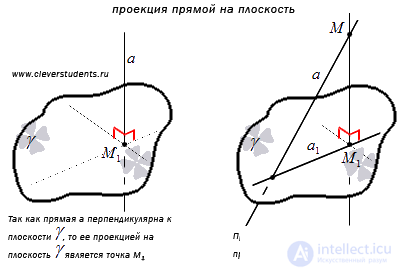
Definition
Projection of a line a onto a plane  call the set of projections of all points of the line a on the plane
call the set of projections of all points of the line a on the plane  .
.
Obviously, the projection of a straight line perpendicular to the plane  on the plane
on the plane  is their point of intersection. It is also quite obvious that the projection of the line a , which intersects the plane
is their point of intersection. It is also quite obvious that the projection of the line a , which intersects the plane  and not perpendicular to this plane, to the plane
and not perpendicular to this plane, to the plane  is a straight line lying in a plane
is a straight line lying in a plane  and passing through the intersection of the line a and the plane
and passing through the intersection of the line a and the plane  .
.
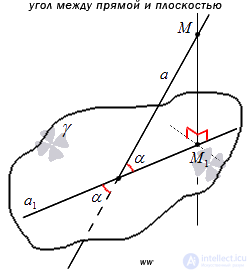
Now we have enough information to give a definition of the angle between a straight line and a plane.
Definition
The angle between a straight line and a plane that intersects this straight line and is not perpendicular to it is the angle between the straight line and its projection onto this plane.
The definition of the angle between the straight line and the plane allows us to conclude that the angle between the straight line and the plane is the angle between two intersecting straight lines: the straight line itself and its projection onto the plane. Therefore, the angle between a straight line and a plane is an acute angle.
The angle between the perpendicular lines and the plane is considered equal  , and the angle between parallel lines and planes is either not determined at all, or is considered equal
, and the angle between parallel lines and planes is either not determined at all, or is considered equal 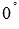 .
.
The conditions of the tasks in which you have to find the angle between a straight line and a plane are quite diverse. Depending on the source data, you have to choose the appropriate solution method. Signs of equality or similarity of figures, the cosine theorem and the definition of sine, cosine and tangent of an angle often help to cope with the task of finding the angle between a straight line and a plane. You can also find the angle between a straight line and a plane using the coordinate method. Let us dwell on it in more detail.
Suppose that in a three-dimensional space a rectangular coordinate system Oxyz is introduced, and the straight line a is defined in it, which intersects the plane  at point M and not perpendicular to the plane
at point M and not perpendicular to the plane  and you need to find the angle
and you need to find the angle 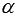 between the line a and the plane
between the line a and the plane  .
.
Let's start with the initial data, from which we will repel when determining the angle between a straight line and a plane by the method of coordinates.
Direct a in a given rectangular coordinate system Oxyz corresponds to some equations of a straight line in space and a directing vector of a straight line in space, and the plane  - an equation of a plane of some kind and a normal vector of a plane. Let be
- an equation of a plane of some kind and a normal vector of a plane. Let be 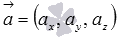 - directing vector of a ,
- directing vector of a , 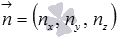 - normal plane vector
- normal plane vector  . So, we will assume that we know the coordinates of the direct vector of the line a and the coordinates of the normal vector of the plane
. So, we will assume that we know the coordinates of the direct vector of the line a and the coordinates of the normal vector of the plane  (if the equations of the line a and the plane are known
(if the equations of the line a and the plane are known  then the coordinates of vectors
then the coordinates of vectors  and
and 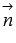 determined by these equations).
determined by these equations).
It remains to obtain a formula that will allow us to calculate the angle between a straight line and a plane from the known coordinates of the direct vector of the straight line and the normal vector of the plane.
Set aside vectors  and
and 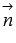 from the point of intersection of the line a and the plane
from the point of intersection of the line a and the plane  . Depending on the coordinates of the vectors
. Depending on the coordinates of the vectors  and
and 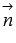 There are four possible locations of these vectors relative to the given straight line and plane. Draw them on the drawing.
There are four possible locations of these vectors relative to the given straight line and plane. Draw them on the drawing.
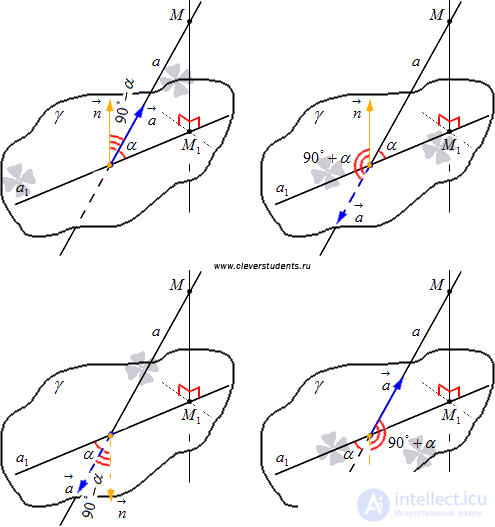
Obviously, if the angle between the vectors  and
and 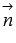 (denote it
(denote it 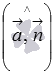 ) sharp, then it complements the desired angle
) sharp, then it complements the desired angle 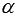 between a straight line and a plane to a right angle, that is,
between a straight line and a plane to a right angle, that is, 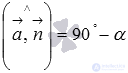 . If
. If 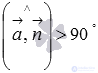 then
then 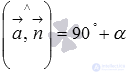 .
.
Since the cosines of equal angles are equal, the last equalities can be written as follows: 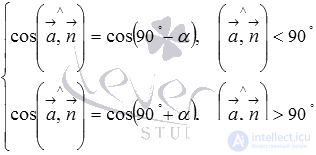
Reduction formulas lead us to equalities 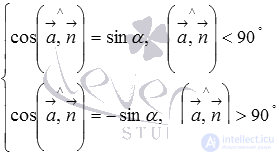 which after transformation take the form
which after transformation take the form 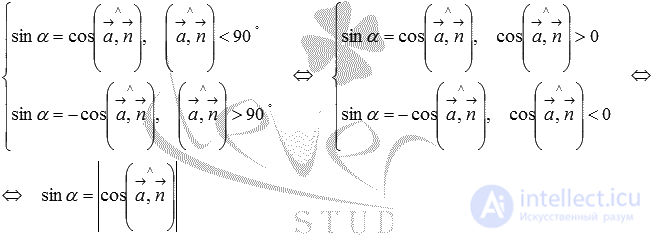
That is, the sine of the angle between the straight line and the plane is equal to the modulus of the cosine of the angle between the directing vector of the straight line and the normal vector of the plane .
In the section on finding the angle between two vectors, we found that the angle between the vectors is equal to the ratio of the scalar product of vectors and the product of the lengths of these vectors, then the formula for calculating the sine of the angle between the straight line and the plane is 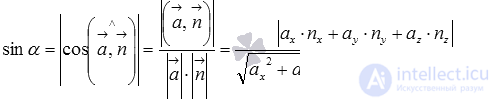 .
.
Therefore, the formula for calculating the angle between a straight line and a plane according to the coordinates of the direct vector of the straight line and the normal vector of the plane is 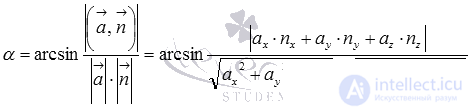 .
.
The basic trigonometric identity allows us to find the cosine of an angle with a known sine. Since the angle between the straight line and the plane is sharp, the cosine of this angle is a positive number and is calculated by the formula 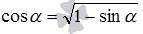 .
.
Now we can find the sine of the angle, the cosine of the angle and the angle itself between the straight line and the plane using the formulas obtained. Let's solve some typical examples.
Example.
Find the angle, sine and cosine of the angle between the line 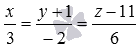 and the plane
and the plane 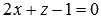 .
.
Decision.
The canonical equations of a straight line in space allow us to immediately obtain the coordinates of the directing vector — they are given by numbers in the denominators of fractions. I.e, 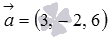 - directing vector straight
- directing vector straight 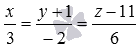 .
.
The general equation of the plane contains the coordinates of the normal vector of the plane in the form of coefficients for variables x , y and z . That is, the normal plane vector 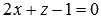 is a vector
is a vector 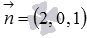 .
.
Substitute the coordinates of vectors  and
and 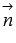 in the formula for calculating the sine of the angle between a straight line and a plane:
in the formula for calculating the sine of the angle between a straight line and a plane: 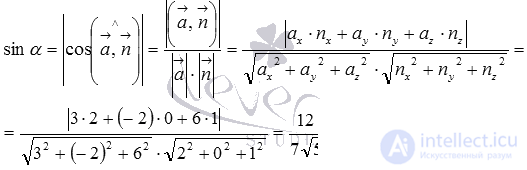
Then 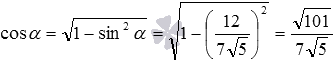 and
and 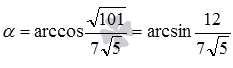 .
.
Answer:
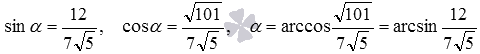
Example.
On vectors 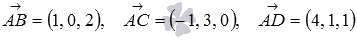 built a pyramid. Find the angle between the straight line AD and the plane ABC .
built a pyramid. Find the angle between the straight line AD and the plane ABC .
Decision.
To calculate the angle between a straight line and a plane using the obtained formula, we need to know the coordinates of the direct vector of the straight line and the normal vector of the plane. The direction vector of the straight line AD is the vector 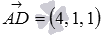 .
.
Normal vector 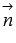 plane abc perpendicular and vector
plane abc perpendicular and vector 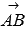 and vector
and vector 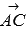 that is, as a normal vector of the ABC plane, one can take the vector product of vectors
that is, as a normal vector of the ABC plane, one can take the vector product of vectors 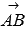 and
and 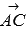 :
: 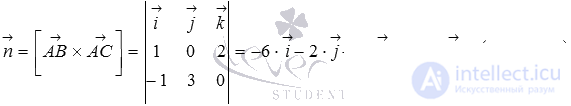
It remains to substitute the coordinates of the vectors in the formula and calculate the required angle between the straight line and the plane: 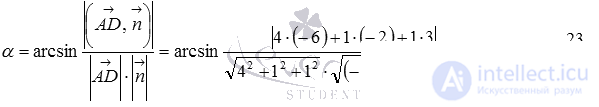
Answer:
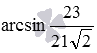
Comments
To leave a comment
Stereometry
Terms: Stereometry