Theorem In a rectangular parallelepiped, the square of any diagonal is equal to the sum of the squares of its three dimensions.
Evidence Consider a rectangular parallelepiped ABCDA`B`C`D`. By the Pythagorean theorem in the triangle AC`C we get:
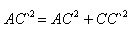
From the right triangle ACB by the Pythagorean theorem we get
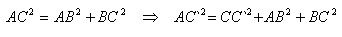
The edges AB, BC and CC `are not parallel, and therefore their lengths are linear dimensions of the parallelepiped. The theorem is proved.
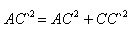
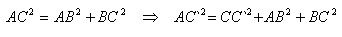
Comments
To leave a comment
Stereometry
Terms: Stereometry