The body of revolution in the simplest case is called such a body, which by planes perpendicular to the axis of rotation, intersect in circles with centers on this line.
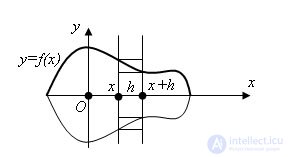
Draw a plane through the axis of the body and enter Cartesian coordinates x, y in this plane, taking the axis of the body as the axis x. The xy plane intersects the surface of the body along a line for which the x axis is the axis of symmetry. Let y = f (x) be the equation of that part of this line that is located above the x axis.
Draw a plane perpendicular to the x axis through the point (x, 0) and denote by V (x) the volume of the part of the body lying to the left of this plane; V (x) is a function of x. The difference V (x + h) - V (x) is the volume of a layer of body thickness h, enclosed between two planes that are perpendicular to the x axis and pass through points with abscissas x and x + h. Let M be the largest, and m the smallest value of the function f (x) on the segment [x, x + h]. Then the body layer under consideration contains a cylinder with radius m and height h and is contained in a cylinder with radius M and the same height h.
therefore
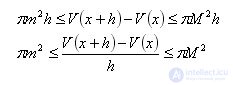
When the height h tends to zero, the left and right sides of the last inequality tend to the same value πf ^ 2 (x). The middle part of this inequality as h tends to 0 tends to the derivative V` (x) of the function V (x). So
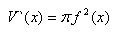
According to the formula of analysis
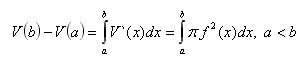
This formula gives the volume of the body part enclosed between parallel planes x = a and x = b.

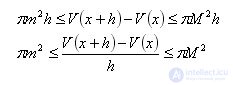
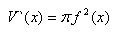
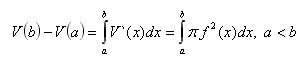
Comments
To leave a comment
Stereometry
Terms: Stereometry