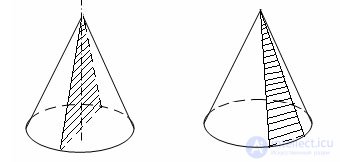
The section of a cone by a plane passing through its top is an isosceles triangle, whose sides are cone-forming. In particular, an isosceles triangle is the axial section of the cone
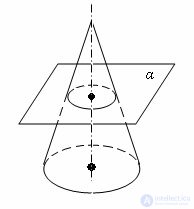
Theorem A plane parallel to the plane of the base of the cone intersects the cone in a circle, and the side surface - on a circle centered on the axis of the cone.
Evidence Let α be a plane parallel to the plane of the base of the cone and intersecting the cone. The transformation of the homothety relative to the apex of the cone, combining the plane α with the plane of the base, combines the section of the cone with the plane α with the base of the cone. Consequently, the section of the cone by the plane is a circle, and the section of the side surface is a circle with the center on the axis of the cone. The theorem is proved.
A plane parallel to the base of the cone and intersecting the cone cuts off a smaller piece from it. The rest is called a
truncated cone .
Comments