Theorem The plane intersecting the pyramid and parallel to its base, cuts off a similar pyramid.
 Evidence
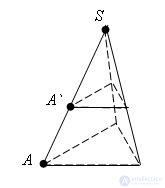
Evidence Let S be the vertex of the pyramid, A be the vertex of the base, and A` be the intersection point of the section plane with the side edge SA. Let us pyramid the homothety transformation relative to the vertex S with the homothety coefficient
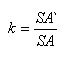
With this homothety, the base plane goes into a parallel plane passing through point A`, i.e. in the cutting plane, and consequently, the whole pyramid is in the part that is cut off by this plane. Since the homothety is a similarity transformation, the cut-off part of the pyramid is a pyramid similar to this one. The theorem is proved.

Comments
To leave a comment
Stereometry
Terms: Stereometry