Parallel straight lines in space. Properties

Theorem

Through a point outside this straight line one can draw a straight line parallel to this straight line, and, moreover, only one.



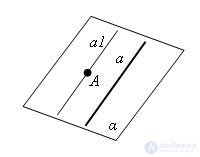Evidence

Let a be a given straight line and A a point not lying on this straight line. Draw through line a and point A plane α. Draw a point a1 parallel to a through the point A in the plane α. Let us prove that the straight line a1, parallel to a, is unique.
Assume that there is another straight line a2 passing through point A and parallel to straight line a. Through the lines a and a2, one can draw the plane α2. The plane α2 passes through the line a and the point A; therefore, by the theorem on a point and a line in space, it coincides with α. Now, by the axiom of parallel lines, a1 and a2 coincide. The theorem is proved.