Homothety in space

Theorem

The transformation of a homothety in space takes any plane that does not pass through the center of the homothety into a parallel plane (or into itself with k = 1).

Evidence

Let O be the center of a homothety and α any plane not passing through the point O. Take any line AB in the plane α. The homothety transformation converts point A to point A` on the ray OA, and point B to point B` on the ray OB, and



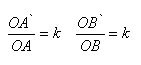
where k is the homothety coefficient. Hence follows the similarity of triangles AOB and A`OB`. The similarity of the triangles implies the equality of the corresponding angles AOB and A `OB, which means that the straight lines AB and A`B` are parallel.
Now take another straight line AC in the plane α. It will go to the parallel straight line A`C` with homothety. Under the considered homothety, the plane α passes to the plane α` passing through the straight lines A`B`, A`C`. Since A`B` is parallel to AB and A`C` parallel to AC, on the basis of parallelism of the planes, the planes α and α` are parallel. The theorem is proved