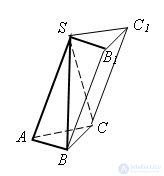
Let SABC be a triangular pyramid with vertex S and base ABC. Let's add this pyramid to a triangular prism with the same base and height. This prism is composed of three pyramids: this SABC pyramid and two more triangular pyramids SCC1B1 and SCBB1.
The second and third pyramids have equal bases - ΔCC1B1 and ΔB1BC and the total height drawn from the top of S. Therefore, they have equal volumes.
The first and third pyramids also have equal bases - ΔSAB and ΔBB1S and coincident heights drawn from the top of C. Therefore, they also have equal volumes.
This means that all three pyramids have the same volume. Since the sum of the volumes is equal to the volume of the prism, the volumes of the pyramids are SH / 3.
The volume of any triangular pyramid is equal to one third of the product of the area of the base to the height:
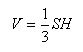

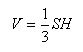
Comments
To leave a comment
Stereometry
Terms: Stereometry