A given body has volume V if there exist simple bodies containing it and simple bodies contained in it with volumes that differ slightly from V.
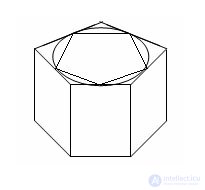
Find the volume of the cylinder with a base radius R and height H.
We construct two straight prisms with height H such that the base of one prism is an n-gon containing a circle, and the base of the second prism is an n-gon contained in a circle. Then the first prism contains a cylinder, and the second prism is contained in the cylinder. With an unlimited increase in n, the areas of polygons approach the area of the circle S (the base of the cylinder) and, consequently, their volumes approach unlimitedly towards SH. Then
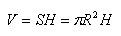
The volume of the cylinder is equal to the product of the base area and height.

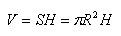
Comments
To leave a comment
Stereometry
Terms: Stereometry